|
|
Nachdem wir im vorherigen Kapitel gesehen haben, dass die Infrarotstrahlung vollständig innerhalb des 15μm-Bandes absorbiert wird, wollen wir in diesem Kapitel untersuchen, was genau mit der absorbierten Strahlung geschieht. Es wurde viel diskutiert, ob die untere Atmosphäre die 342W/m2 aus Abbildung 1-1 in Richtung Erde überhaupt abstrahlen kann. Auf der einen Seite kann die atmosphärische Gegenstrahlung gemessen werden, auf der anderen Seite steht das Argument der im Kapitel 7.3 beschriebenen Stoß- oder Druckverbreiterung der Spektrallinien. Danach wird durch häufige Stöße die Wahrscheinlichkeit stark gemindert, dass ein zur Schwingung angeregtes CO2-Molekül überhaupt die Zeit dazu findet, seine Schwingungsenergie durch Abstrahlung eines Photons abzugeben. Um uns diesem Thema zu nähern, kommen wir noch einmal auf das Schwingkreismodell von Kapitel 7 zurück. So wie jede elektromagnetische Strahlungsquelle durch Abstrahlung bzw. Dämpfung Energie verliert, entvölkert sich ein angeregter Molekülzustand. Das Ergebnis sind Spektrallinien, deren Form sich nach denselben Formeln berechnen lässt wie die Resonanzkurve eines Schwingkreises. Um zu verstehen was mit der absorbierten Strahlung geschieht, denken wir uns in einem Gedankenexperiment alle CO2-Moleküle gleichzeitig angeregt und addieren jeweils die Amplituden der schwingenden Moleküle. Natürlich werden es im Laufe der Zeit immer weniger und wir erhalten das Bild einer gedämpften Schwingung (siehe Abbildung 10-1), deren Amplitude nach einer e-Funktion abnimmt. Man kann sich sämtliche Molekularschwingkreise als einen einzigen gedämpften elektrischen Schwingkreis nach Abbildung 10-2 vorstellen, dessen Kondensator C durch Stoß oder durch auftreffende Photonen geladen wird.
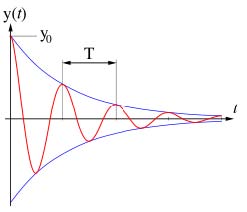
Abb. 10-1: gedämpfte Schwingung, (Quelle: Wikipedia Gedämpfte Schwingung)
Das Stauchen oder Auseinanderziehen der Atomkerne der Moleküle entspricht dabei der veränderten elektrischen Ladung des Kondensators C. Durch die Bewegung der Ladung wird nach dem Induktionsgesetz eine Spannung induziert. Dieses Verhalten wird durch die Spule L beschrieben. Die Dämpfung des Schwingkreises wird durch zwei Mechanismen hervorgerufen:
| 1) |
durch Abstrahlung elektromagnetischer Wellen |
| 2) |
durch stoßbedingte Energieabgabe an benachbarte N2- bzw. O2-Moleküle |
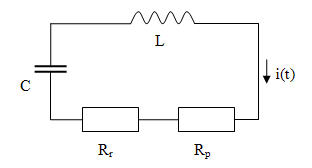
Abb. 10-2: gedämpfter Reihenschwingkreis
Beide Mechanismen werden durch zwei verschiedene Dämpfungswiderstände berücksichtigt. Der Dämpfungswiderstand Rr wird durch die natürliche Linienbreite – also durch Abstrahlung – hervorgerufen und der Dämpfungswiderstand Rp entspricht der Druckverbreiterung durch Stöße. Die Leistungsverteilung auf beide Widerstände ist ein Maß dafür, wie viel der absorbierten Strahlungsenergie das CO2 in der Atmosphäre überhaupt wieder als Strahlung abgeben kann. Um diese Frage klären zu können, wird zunächst die Differentialgleichung für die Schaltung nach Abbildung 10-2 aufgestellt. Die Teilwiderstände Rr und Rp werden zunächst als Gesamtdämpfungswiderstand R aufgefasst. Es gilt zunächst für eine Reihenschaltung, dass die Summe der Einzelspannungen Null sein muss:
| $$U_C + U_R + U_L = 0$$ |
(10.1) |
Für die Spannung am Kondensator UC gilt:
| $$U_C = \frac{1}{C} \cdot \int {i(t)dt} $$ |
(10.2) |
Für die Spannung an der Spule UL gilt das Induktionsgesetz:
| $$U_L = L \cdot \frac{{di(t)}}{{dt}}$$ |
(10.3) |
Für die Spannung am Widerstand UR gilt das ohmsche Gesetz:
| $$U_R = R \cdot i(t)$$ |
(10.4) |
Werden nun (10.2), (10.3) und (10.4) in (10.1) eingesetzt und einmal differenziert ergibt sich die gesuchte Differentialgleichung für den fließenden Strom i(t):
| $$\frac{1}{C} \cdot \int {i(t)dt} + L \cdot \frac{{di(t)}}{{dt}} + R \cdot i(t) = 0$$ |
→ |
$$\frac{1}{C} \cdot i(t) + L \cdot \frac{{d^2 i(t)}}{{dt^2 }} + R \cdot \frac{{di(t)}}{{dt}} = 0$$ |
|
| $$\frac{{d^2 i(t)}}{{dt^2 }} + \frac{R}{L} \cdot \frac{{di(t)}}{{dt}} + \frac{1}{{L \cdot C}} \cdot i(t) = 0$$ |
(10.5) |
| Nach der Thomsonschen Schwingungsgleichung gilt: |
$$\frac{1}{{L \cdot C}} = \omega _0^2 $$ |
|
Der Ausdruck R/L wird nun mit der Resonanzkreisfrequenz ω0 erweitert:
| $$\frac{{d^2 i(t)}}{{dt^2 }} + \omega _0 \cdot d \cdot \frac{{di(t)}}{{dt}} + \omega _0^2 \cdot i(t) = 0 |
|
| Elektrotechnisch kann man nun den Dämpfungsfaktor d einführen: |
$$\frac{R}{{\omega _0 \cdot L}} = d$$ |
(10.6) |
| $$\frac{{d^2 i(t)}}{{dt^2 }} + \omega _0 \cdot d \cdot \frac{{di(t)}}{{dt}} + \omega _0^2 \cdot i(t) = 0$$ |
(10.7) |
Die Lösung dieser Differentialgleichung soll ohne Herleitung für d << 1 und mit dem Anfangswert i(t=0) = i0 sofort angegeben werden:
| $$i(t) = i_0 \cdot e^{ - \omega _0 \cdot \frac{d}{2} \cdot t} \cdot \cos \left( {\omega _0 \cdot t} \right)$$ |
(10.8) |
Gleichung (10.8) hat den Verlauf nach Abbildung 10-1, wobei für die Dämpfungszeitkonstante τ gilt:
| $$\tau = \frac{2}{{d \cdot \omega _0 }}$$ |
(10.9) |
Für die im Schwingkreis nach Abbildung 10-2 umgesetzten Wirkleistungen Pr und Pp gilt nach (10.6):
| $$P_r = i(t)^2 \cdot R_r = i(t)^2 \cdot \omega _0 \cdot L \cdot d_r $$ |
(10.10) |
| $$P_p = i(t)^2 \cdot R_p = i(t)^2 \cdot \omega _0 \cdot L \cdot d_p $$ |
(10.11) |
Dividiert man (10.10) und (10.11) kommt man auf das im gedämpften Schwingkreis umgesetzte Leistungsverhältnis:
| $$\frac{{P_p }}{{P_r }} = \frac{{R_p }}{{R_r }} = \frac{{d_p }}{{d_r }}$$ |
(10.12) |
Die Dämpfungsfaktoren der natürlichen Linienbreite dr und die der druckverbreiterten Linie dp bei +15°C sind uns nach (7.14) und (9.1) bekannt:
| $$d_r = 1,5 \cdot 10^{ - 11} $$ |
(10.13) |
| $$d_p = \frac{{\Delta f_{1/2} }}{{f_0 }} = \frac{{4,569GHz}}{{20000GHz}} = 2,28 \cdot 10^{ - 4} $$ |
(10.14) |
Damit gilt für das Leistungsverhältnis der durch Stöße abgegebenen Leistung zur tatsächlich abgestrahlten Leistung nach (10.12), (10.13) und (10.14):
| $$\frac{{P_p }}{{P_r }} = \frac{{2,28 \cdot 10^{ - 4} }}{{1,5 \cdot 10^{ - 11} }} = 1520000$$ |
(10.15) |
Damit beträgt die Wahrscheinlichkeit pr, dass ein angeregtes CO2-Molekül in Erdnähe ein Photon abstrahlen kann, nur:
| $$p_r = \frac{1}{{1520000}} = 6,6 \cdot 10^{ - 8} = 0,066ppm$$ |
(10.16) |
Zum selben Ergebnis kommt man durch die Betrachtung der Dämpfung nach (10.8) und (10.9). Die Lebenszeit der Abstrahlung τr wird durch Stöße auf τp begrenzt. Daher kann berechnet werden, wie viele CO2-Moleküle innerhalb τp mit der Zeitkonstante τr abstrahlen. Verwendet wird die übliche Tiefpassgleichung mit den Werten von (7.13) und (7.46):
| $$p_r = 1 - e^{ - \frac{{\tau _p }}{{\tau _r }}} = 1 - e^{ - \frac{{3,55 \cdot 10^{ - 11} s}}{{5,3 \cdot 10^{ - 4} s}}} = 6,6 \cdot 10^{ - 8} = 0,066ppm$$ |
|
Die absorbierte Strahlungsenergie kann also nur noch sehr eingeschränkt wieder direkt abgestrahlt werden. Dieses Verhalten ist in der Physik unter dem Begriff Dissipation bekannt. Im Internetlexikon Wikipedia steht unter dem Begriff "Dissipation":
Dissipation, heißt wörtlich "Zerstreuung", bezeichnet in der Physik den Vorgang in einem dynamischen System, bei dem z. B. durch Reibung die Energie einer makroskopisch gerichteten Bewegung, die in andere Energieformen umwandelbar ist, in thermische Energie übergeht, d. h. in Energie einer ungeordneten Bewegung der Moleküle, die dann nur noch teilweise umwandelbar ist. Ein solches System heißt dissipativ. Dieser Begriff kommt in den physikalischen Gebieten der Thermodynamik und der Akustik oder allgemein in der Wellenlehre vor. Ein Beispiel für ein dissipatives System ist die gedämpfte Schwingung.
Die vom CO2 absorbierte Wärmestrahlung wird in der unteren Atmosphäre durch Erhöhung der Molekularbewegung der atmosphärischen Gase gespeichert. Dies führt zu einer Temperaturerhöhung der Atmosphäre, die zusätzlich zur Konvektion wirksam wird. Durch die Temperaturerhöhung steigt aber auch die Wahrscheinlichkeit, dass ein CO2-Molekül durch Zusammenstoß mit einem schnellen N2- oder O2-Molekül zum Schwingen angeregt wird. Beim nächsten Zusammenstoß wird das schwingende CO2-Molekül mit hoher Wahrscheinlichkeit wieder abgeregt.
Nun soll abgeschätzt werden, wie viel Strahlungsleistung in 1m3 Luft bei 1bar und +15°C von den CO2-Molekülen bei einer Konzentration von 380ppm abgegeben wird. Dazu muss im ersten Schritt die Anzahl der strahlenden Moleküle ermittelt werden. Unter Normalbedingungen (0°C, 1bar) entspricht 1mol eines Gases einem Volumen von 22,4l. Bei +15°C ist es entsprechend mehr. Man kann folgende Verhältnisgleichung aufstellen:
| $$\frac{{22,4l}}{{273K}} = \frac{x}{{288K}}$$ |
→ |
$$x = 23,63l = 0,02363m^3 $$ |
(10.17) |
Da ein mol 6,022·1023 Teilchen enthält, lässt sich sofort die Anzahl der Luftmoleküle nL pro m3 angeben:
| $$n_L = \frac{{6,022 \cdot 10^{23} }}{{0,02363m^3 }} = 2,548 \cdot 10^{25} m^{ - 3} $$ |
(10.18) |
Nach Tabelle 5-1 beträgt das Verhältnis schwingender zu nicht schwingender CO2-Moleküle bei +15°C 1:14. Mit (10.16) und einer CO2-Konzentration von 380ppm ist die Anzahl der strahlenden Moleküle nr:
| $$n_r = 2,548 \cdot 10^{25} m^{ - 3} \cdot 0,00038 \cdot 6,6 \cdot 10^{ - 8} \cdot \frac{1}{{15}} = 4,26 \cdot 10^{13} m^{ - 3} $$ |
(10.19) |
Wenn alle Moleküle gleichzeitig abstrahlen, liegt die Strahlungsarbeit bei:
| $$W_r = n_r \cdot h \cdot f_{v2} = 4,26 \cdot 10^{13} m^{ - 3} \cdot 6,626 \cdot 10^{ - 34} Js \cdot 20,01THz = 5,65 \cdot 10^{ - 7} \frac{{Ws}}{{m^3 }}$$ |
(10.20) |
Für die Berechnung der Leistung muss nun die Zeit ermittelt werden, bis die Moleküle wieder "aufgeladen" sind. Diese "Aufladung" geschieht thermisch durch Stöße mit Luftmolekülen hoher kinetischer Energie. Die Luftmoleküle haben eine mittlere kinetische Energie, die sich durch eine mittlere translatorische Geschwindigkeit ausdrückt. Die individuelle Geschwindigkeit folgt jedoch der Maxwell-Boltzmann-Verteilungsdichte nach (10.21):
| $$p(v) = \sqrt {\frac{2}{\pi }} \cdot \sqrt {\left( {\frac{{m_L }}{{k_B \cdot T}}} \right)^3 } \cdot v^2 \cdot e^{ - \frac{{m_L \cdot v^2 }}{{2 \cdot k_B \cdot T}}} $$ |
(10.21) |
Die mittlere Masse eines Luftmoleküls mL leitet sich aus den gewichteten relativen Massen von N2 (80%) und O2 (20%) und der absoluten Masse des Wasserstoffatoms mH = 1,67·10-27kg her (h ist das Plancksche Wirkungsquantum von 6,626·10-34Js und kB ist die Boltzmannkonstante von 1,381·10-23J/K).
| $$m_L = \left( {0,8 \cdot 28 + 0,2 \cdot 32} \right) \cdot 1,67 \cdot 10^{ - 27} kg = 48,1 \cdot 10^{ - 27} kg$$ |
(10.22) |
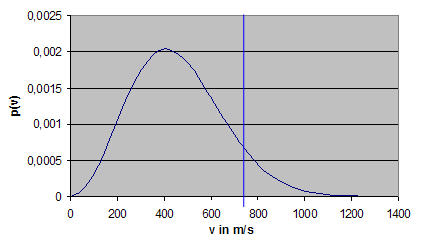
Abb. 10-3: Geschwindigkeitsverteilungsdichte von Luft
Die Masse von (10.22) in (10.21) eingesetzt ergibt bei +15°C die Geschwindigkeitsverteilung nach Abbildung 10-3. Durch Integration von (10.21) erhält man die zugehörige Verteilungsfunktion F(v). Sie drückt die Wahrscheinlichkeit P aus, dass die Geschwindigkeit eines Moleküls unterhalb des betrachteten Punktes (türkisfarbige Linie in Abb. 10-4) liegt. F(v) ist nicht als geschlossene Funktion darstellbar. Daher wurde die Integration numerisch durchgeführt. Das Ergebnis ist in Abbildung 10-4 dargestellt:
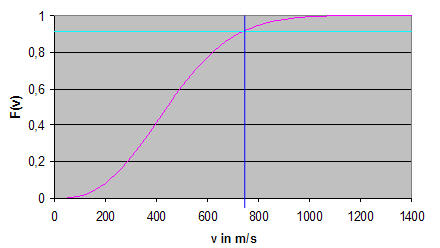
Abb. 10-4: Geschwindigkeitsverteilungsfunktion von Luft
Die blaue Linie markiert die nötige, in Geschwindigkeit umgerechnete, Anregungsenergie für die Deformationsschwingung des CO2-Moleküls. Sie liegt bei:
| $$\frac{{m_L \cdot v_{V2\min }^2 }}{2} = h \cdot f_{V2} $$ |
|
| $$v_{V2\min } = \sqrt {\frac{{2 \cdot h \cdot f_{V2} }}{{m_L }}} = \sqrt {\frac{{2 \cdot 6,626 \cdot 10^{ - 34} Js \cdot 20,01THz}}{{48,1 \cdot 10^{ - 27} kg}}} = 742,5\frac{m}{s}$$ |
(10.23) |
Die Wahrscheinlichkeit P(vV2min), dass eine zur Schwingungserregung notwendige Geschwindigkeit anzutreffen ist, liegt nach einer Excel-Simulation bei:
| $$P(v > 742,5m/s) = 1 - F(742,5m/s) = 0,0839$$ |
(10.24) |
Dass bedeutet, dass 8,39% der Luftmoleküle die nötige kinetische Energie besitzen, um ein CO2-Molekül zur Deformationsschwingung anzuregen. So soll als nächstes die Zeitspanne zwischen zwei Stößen abgeschätzt werden.
Die zum aller größten Teil zweiatomigen Luftmoleküle besitzen bei "normalen" Temperaturen drei Freiheitsgrade der Translation und zwei Freiheitsgrade der Rotation (die Vibration ist "eingefroren"). Daher berechnet sich die innere Energie eines Luftmoleküls UL nach (3.1) zu:
| $$U_L = \frac{5}{2} \cdot k_B \cdot T$$ |
(10.25) |
Dabei ist kB = 1,381·10-23J/K wieder die Boltzmannkonstante und T die absolute Temperatur. Die innere Energie drückt sich in der mittleren kinetischen Energie Ekin aus. Zur Geschwindigkeit des Luftmoleküls im Raum tragen aber nur die Translationsfreiheitsgrade bei, also nur 3/5 von UL. Damit kann man zur Ermittlung der mittleren Geschwindigkeit eines Luftmoleküls folgende Energiebilanz aufstellen:
| $$\overline E _{kin} = \frac{3}{5} \cdot U_L $$ |
(10.26) |
Die mittlere kinetische Energie eines Luftmoleküls und berechnet sich nach der üblichen Formel:
| $$\overline E _{kin} = \frac{1}{2} \cdot m_L \cdot \overline v ^2 $$ |
(10.27) |
Wobei v_Strich die mittlere Geschwindigkeit der Luftmoleküle darstellt. Nach (10.22), (10.25), (10.26) und (10.27) lässt sich v_Strich bei +15°C folgendermaßen berechnen:
| $$\frac{1}{2} \cdot m_L \cdot \overline v ^2 = \frac{3}{2} \cdot k_B \cdot T$$ |
→ |
$$\overline v = \sqrt {\frac{{3 \cdot k_B \cdot T}}{{m_L }} = } \sqrt {\frac{{3 \cdot 1,381 \cdot 10^{ - 23} \frac{J}{K} \cdot 288K}}{{4,81 \cdot 10^{ - 26} kg}}} = 498\frac{m}{s}$$ |
(10.28) |
Um nun zur mittleren Stoßzeit zu kommen, braucht man die freie Weglänge, die ein Luftmolekül unter normalem atmosphärischem Druck zurücklegen kann, bevor es mit einem anderen Luftmolekül zusammenstößt. Betrachtet man näherungsweise die Luftmoleküle als Kugeln mit dem Radius r, so tritt dann ein Stoß ein, wenn sich die Mittelpunkte zweier Kugeln näher als die Summe beider Radien r1 und r2 kommen. Zum selben Ergebnis kommt man, wenn ein Molekül als Punkt und das andere als Scheibe mit dem Radius r1+r2 aufgefasst wird.
Das Buch "Molekülphysik und Quantenchemie" (Haken/Wolf, Springer-Verlag, Heidelberg, 1991, S.10) gibt folgende Moleküldurchmesser für die Hauptatmosphärenbestandteile an:
| N2: |
0,38nm |
| O2: |
0,30nm |
| CO2: |
0,34nm |
Damit ergibt sich über die prozentuale Luftzusammensetzung gewichtet für ein mittleres Luftmolekül folgender Durchmesser:
| $$d_L = 0,8 \cdot 0,38nm + 0,2 \cdot 0,3nm = 0,36nm$$ |
(10.29) |
Da der Durchmesser von CO2 fast genau so groß ist, soll der Einfachheit halber in dieser Abschätzung generell mit 0,36nm für den Durchmesser eines Luftmoleküls gerechnet werden. Der Flächeninhalt einer Scheibe mit dem Radius r1+r2 berechnet sich dann zu:
| $$A_L = \frac{\pi }{4} \cdot \left( {2 \cdot d_L } \right)^2 = \pi \cdot \left( {0,36nm} \right)^2 = 0,407nm^2 = 4,07 \cdot 10^{ - 19} m^2 $$ |
(10.30) |
Die freie Weglänge l ergibt sich aus dem Volumen V, welches ein Luftmolekül bei gegebenem Druck für sich zur Verfügung hat, ohne an ein anderes Molekül zu stoßen. Damit ergibt sich für die freie Weglänge:
Weil sich aber alle Moleküle etwa gleich schnell bewegen, wird sich die freie Weglänge nach dem Buch "Gerthsen Physik" (H. Vogel, Springer-Verlag, Heidelberg, 19. Auflage, 1997, S.222) um den Korrekturfaktor 1/√2 verringern. Somit ergibt sich:
| $$l = \frac{V}{{A_L \cdot \sqrt 2 }}$$ |
(10.31) |
Das für ein Molekül zur Verfügung stehende Volumen ist der reziproke Wert der Teilchendichte von Luft unter normalem Luftdruck und +15°C Temperatur von (10.18).
| $$V = \frac{1}{{n_L }} = \frac{1}{{2,548 \cdot 10^{25} m^{ - 3} }} = 3,924 \cdot 10^{ - 26} m^3 $$ |
|
Nun lässt sich die freie Weglänge berechnen zu:
| $$l = \frac{{3,924 \cdot 10^{ - 26} m^3 }}{{4,07 \cdot 10^{ - 19} m^2 \cdot \sqrt 2 }} = 68,17nm$$ |
(10.32) |
Damit berechnet sich die mittlere Zeit zwischen zwei Stößen nach (10.28) und (10.32) zu:
| $$t = \frac{l}{{\overline v }} = \frac{{68,17nm}}{{498\frac{m}{s}}} = 0,137ns$$ |
(10.33) |
Unter Berücksichtigung von (10.24) wird sich die effektive Zeit bis zur Anregung verlängern, weil nur 8,39% aller Stöße die notwendige Energie besitzen. Außerdem kann der energiereiche Stoß nicht nur zur Schwingung sondern auch zur Erhöhung der translatorischen Energie bzw. zur Erhöhung der Rotationsenergie führen. Weil alle Arten der inneren Energie die gleiche Wahrscheinlichkeit besitzen, ist noch ein Faktor von 2/7 einzufügen (3 Freiheitsgrade der Translation, 2 Freiheitsgrade der Rotation, 2 Freiheitsgrade der Deformationsschwingung). Daher berechnet sich die mittlere Zeitspanne für eine Abstrahlung tr nach (10.24) und (10.33) zu:
| $$t_r = \frac{{0,137ns}}{{0,0839 \cdot \frac{2}{7}}} + 0,0355ns = 5,75ns$$ |
(10.34) |
Hinzugefügt wurde noch die mittlere Lebensdauer des angeregten Zustandes nach (7.46). Nun kann aus (10.20) die mittlere Strahlungsleistung pro m3 berechnet werden:
| $$P_r = \frac{{W_r }}{{t_r }} = \frac{{5,65 \cdot 10^{ - 7} \frac{{Ws}}{{m^3 }}}}{{5,75 \cdot 10^{ - 9} s}} = 98,3\frac{W}{{m^3 }}$$ |
(10.35) |
Denkt man sich eine 1m starke Luftschicht, die aus Würfeln von 1m Kantenlänge zusammengesetzt ist, dann wird die seitliche Strahlung innerhalb der Schicht verbleiben und nach oben und unten wird maximal 1/6 der Strahlung von (10.35) austreten. Die 1m starke Schicht strahlt also mit:
| $$I\left( {1m} \right) = \frac{{P_r }}{6} = \frac{{98,3}}{6} = 16,4\frac{W}{{m^2 }}$$ |
(10.36) |
Wenn man die nächste Luftschicht betrachtet, deren Druck und Temperatur zwar etwas geringer sind, so wird doch die Strahlung in Richtung beider Ränder stärker werden. Jedoch wird sie nicht linear mit der Schichtdicke ansteigen, da es zur Absorption innerhalb der Schicht kommen wird. Mit steigender Schichtdicke wird daher eine Art Sättigung zu erwarten sein.
Innerhalb der Atmosphäre wird durch die Strahlung der CO2-Moleküle die Wärmeleitfähigkeit zusätzlich zur Konvektion erhöht. Die Wärme kann schneller in höhere Atmosphäreschichten transportiert werden. Daher ist es auch fraglich, ob sich bei Erhöhung der CO2-Konzentration die oberen Atmosphärenschichten tatsächlich, so wie in "Chemie und Umwelt" (Reinhardt/Heintz, Vieweg & Sohn Verlagsgesellschaft mbH, Braunschweig, 1990, S.36), postuliert, abkühlen werden. Die abgestrahlte Energie kann ja nun auch schneller wieder von unten ersetzt werden.
Da mit steigender Höhe der Druck sinkt, werden auch die Stöße zwischen den Molekülen seltener. Es werden weniger CO2-Moleküle zum Schwingen angeregt, dafür steigt die Wahrscheinlichkeit, dass sie auch abstrahlen können, weil die Schwingungsdauer in die Größenordnung der Halbwertszeit kommt. Man kann daher in großen Höhen ein schönes Emissionsspektrum des CO2 messen.
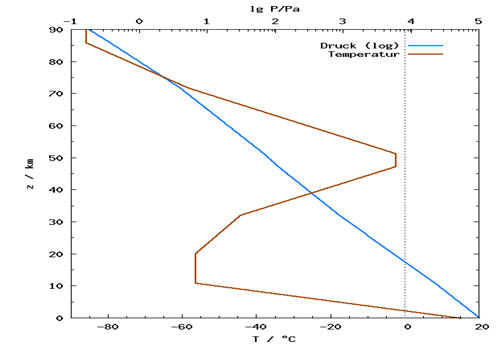
Abb. 10-5: Temperatur- und Druckprofil der unteren Atmosphärenschichten, (Quelle: Wikipedia, Luftdruck)
Nach Abbildung 7-5 geschieht das bei einem Druck von ca. 20mbar. Dieser Druck markiert den übergang vom Gauß- zum Lorenzprofil, also von der Dopplerverbreiterung zur Druckverbreiterung. Geht man mit diesem Druck in das Diagramm aus Abbildung 10-5 so erhält man:
| $$\lg \frac{{20mbar}}{{bar}} = \lg \frac{{2000Pa}}{{Pa}} = 3,3 \Rightarrow \approx 22km$$ |
(10.37) |
Damit liegt der Beginn der "CO2-Strahlungszone" deutlich über dem Ende der Troposphäre in der Stratosphäre und damit in einem Bereich der Atmosphäre, der auf das Wettergeschehen keinen Einfluss mehr hat (siehe Abbildung 10-6). Wikipedia schreibt zum Thema "Troposphäre":
"Die Troposphäre ist die unterste Schicht der Atmosphäre und Teil der Homosphäre. Die Troposphäre reicht vom Erdboden bis zur Tropopause. Ihre Dicke beträgt etwa 8km an den Polen, wo sie im Winter bis zu 2km niedriger ist als im Sommer, und 18km am Äquator. In der Troposphäre sind etwa 90% der gesamten Luft sowie beinahe der gesamte Wasserdampf der Atmosphäre enthalten. Da sich in ihr der Großteil des Wetters abspielt, spricht man auch von der Wetterschicht der Atmosphäre.
Die Troposphäre wird nur in geringem Maße direkt durch Sonnenstrahlen erwärmt. Der größte Teil der Wärme wird vom Erdboden aufgenommen, weswegen die Lufttemperatur im Schnitt um etwa 6,5°C pro Kilometer Höhe abnimmt (Definition der Standardatmosphäre). Dies nennt man den vertikalen Temperaturgradienten. Im Einzelnen beträgt die Temperaturabnahme in trocken-adiabatischen (= wolkenlosen) Abschnitten durchschnittlich 1 Grad auf je 100m, im feucht-adiabatischen (wolken- und nebelreichen) Raum sind es pro 100m etwa 0,6 Grad.
An der Tropopause beträgt die Temperatur um –75°C (am Äquator) bis –45°C (an den Polen). Das heißt aber auch, dass warme Gase hochsteigen und kalte absinken. Die Luft wird dadurch durchmischt, die Entstehung von Wetter wird möglich. Deswegen spielen sich alle Vorgänge, die das Wetter beeinflussen, in der Troposphäre ab. Durch den vorhandenen Wasserdampf werden Wolken gebildet, Regen entsteht und die Troposphäre wird von gelösten Gasen und Feststoffen gereinigt.
Die nächst höhere Luftschicht über der Troposphäre ist die Stratosphäre (bis 50km Höhe), mit der nur ein geringer Luftaustausch stattfindet, da hier zunächst eine sogenannte Isothermie herrscht (Temperatur bleibt mit zunehmender Höhe gleich). Ab dem Beginn der Ozonschicht (zwischen 20 und 50km Höhe) nimmt die Temperatur sogar wieder zu (Inversion) bis etwa 0°C. Die Grenzschicht zwischen Troposphäre und Stratosphäre wird als Tropopause bezeichnet."
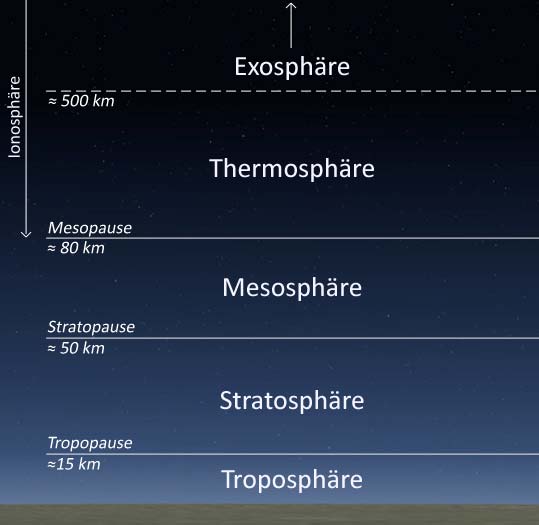
Abb. 10-6: Aufbau der Erdatmosphäre, (Quelle: Wikipedia Troposphäre)
Interessant ist in Abbildung 10-5 der Bereich ab einer Höhe von ca. 20km in der Stratosphäre. Da steigt die Temperatur mit wachsender Höhe von -55°C bis auf -3°C an. Diese Temperaturerhöhung ist darauf zurückzuführen, dass Ozon hier die kurzwellige Höhenstrahlung der Sonne absorbiert und thermalisiert. Das führt dazu, dass auf der Erde von dieser Strahlung nur noch ein Bruchteil ankommt und damit das Leben geschützt wird. Wahrscheinlich ist es sogar so, dass die vom CO2 ins Weltall emittierte Strahlungsleistung weitgehend von der vom Ozon thermalisierten Sonnenenergie aufgebracht wird. Gestützt wird diese Vermutung durch die Satellitenmessungen aus Abbildung 10-7. Das Emissionsspektrum des CO2 ist deutlich auf der Temperaturkurve von 220K (= -53°C) zu erkennen und zwar unabhängig vom Bewölkungsgrad und damit unabhängig vom Emissionsgrad der Erdoberfläche.
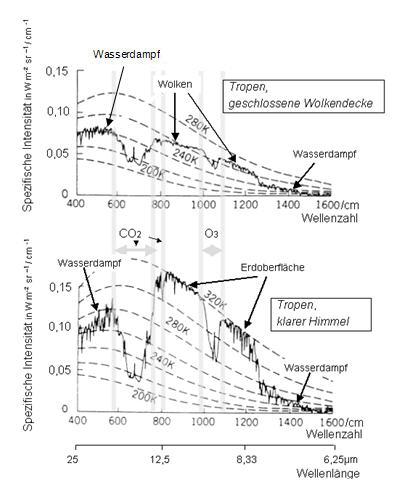
Abb. 10-7: Vom Satelliten gemessene Emissionsspektren, (Quelle: Heinz Thieme, Die Erdatmosphäre - ein Wärmespeicher)
Die Strahlung in dieser Atmosphärenschicht ist vermutlich genauso gesättigt, wie die Absorption in den unteren Atmosphärenschichten. Eine Konzentrationserhöhung des CO2 wird wohl nur das Spektrum marginal verbreitern durch Aktivierung weniger zusätzlicher Spektrallinien an den Rändern des Spektrums (siehe nächstes Kapitel). Jede Schicht strahlt eben entsprechend ihrer Temperatur.
Zusammengefasst lässt sich sagen, dass eintreffende Infrarotstrahlung in den Absorptionsbanden des CO2 in den unteren Atmosphärenschichten vollständig absorbiert wird. Fast alle durch Absorption angeregten CO2-Moleküle geben ihre Schwingungsenergie hier auch durch Stöße an andere Luftmoleküle wieder ab. Das hebt die innere Energie der Luft und damit die Temperatur. Mit steigender Temperatur erhöht sich aber der Anteil von Molekülen mit hoher kinetischer Energie, so dass das Verhältnis von schwingenden zu nicht schwingenden CO2-Molekülen steigt. Damit erhöht sich die Wahrscheinlichkeit der Strahlungsemission.
Anders verhält es sich mit den Wolken. Da hier das Wasser nicht im gasförmigen sondern im flüssigen Aggregatzustand in feiner Tröpfchenform vorliegt, strahlen und absorbieren Wolken im gesamten Frequenzband. Damit bewirkt ein bewölkter Himmel, dass auf der einen Seite eine Erwärmung der Erde durch Sonnenstrahlung erschwert wird, dass aber auf der anderen Seite nachts auch die Abkühlung erschwert wird. So erzeugt Bewölkung kühle Tage und milde Nächte.
|







