|
|
Eine Berechnung des Treibhauseffekts findet sich in dem 1990 herausgegeben Buch "Chemie und Umwelt" (Reinhardt/Heintz, Vieweg & Sohn Verlagsgesellschaft mbH, Braunschweig, 1990, S.28 ff.). Es wird dem Leser als Studienbuch für Chemiker, Physiker, Biologen und Geologen vorgestellt. Der Treibhauseffekt war zur damaligen Zeit in der Öffentlichkeit noch wenig bekannt und doch wurden die politischen Weichen für eine CO2 Reduktion in der Bundesrepublik bereits zu diesem Zeitpunkt gestellt. Der hier vorgestellte Rechenweg kann als Basis für alle Klimamodelle und Temperaturerhöhungs-szenarien angesehen werden. Letztendlich begründen sich hiermit auch alle Einschränkungen, die uns als Folge des Klimaschutzes auferlegt werden. In "Chemie und Umwelt" (Reinhardt/Heintz, Vieweg & Sohn Verlagsgesellschaft mbH, Braunschweig, 1990, S.39) wird in relativen Einheiten (rE) gerechnet. In diesem Werk werden stattdessen die absoluten Werte aus Abbildung 1-1 verwendet.
Zur Berechnung des Treibhauseffekts wird von der Strahlungsbilanz und deren Zusammenhang mit der Temperatur auf der Erdoberfläche ausgegangen. Nach dem Stefan-Boltzmann-Gesetz strahlt ein ideal schwarzer Körper mit der Temperatur T (in Kelvin) Energie mit der Intensität I ab:
| $$I = \sigma \cdot T^4$$ |
(2.1) |
Dabei ist σ = 5,67·10-8 W/(m2·K4) die so genannte Stefan-Boltzmann-Konstante. Die Intensität wird in der Einheit W/m2 angegeben und bezeichnet die pro Fläche abgestrahlte Leistung. Unter einem schwarzen Körper ist ein hypothetischer, idealisierter Körper zu verstehen, der jegliche auf ihn treffende elektromagnetische Strahlung bei jeder Frequenz vollständig absorbiert und entsprechend seiner Temperatur wieder vollständig emittiert. Die Sonne und auch die Erdoberfläche werden in "Chemie und Umwelt" als solche schwarze Strahler angesetzt.
Um bestimmen zu können, wie viel der abgestrahlten Sonnenenergie auf der Erde ankommt, muss zunächst die Intensität der Sonnenstrahlung IS nach (2.1) mit dem Oberflächeninhalt AS der Sonnenkugel mit dem Radius rS multipliziert werden. Damit erhält man die abgestrahlte Gesamtleistung der Sonne LS.
| $$L_S = I_S \cdot A_S = \sigma \cdot T_S^4 \cdot 4 \cdot \pi \cdot r_S^2 $$ |
(2.2) |
Mit dem Sonnenradius rS = 7·108m und der mittleren Sonnentemperatur TS = 5770K berechnet sich nach (2.2) die abgestrahlte Gesamtleistung der Sonne zu:
| $$L_S = 5,67 \cdot 10^{ - 8} \frac{W}{{m^2 \cdot K^4 }} \cdot \left( {5770K} \right)^4 \cdot 4 \cdot \pi \cdot \left( {7 \cdot 10^8 m} \right)^2 = 3,87 \cdot 10^{26} W$$ |
(2.3) |
(Die mittlere Sonnentemperatur wurde so gewählt, dass der in Kapitel 1 genannte Wert der Solarkonstante von 1368W/m2 als Ergebnis herauskommt.) Die Intensität der auf der Erde ankommenden Sonnenstrahlung wird als die schon aus Kapitel 1 bekannte Solarkonstante S0 bezeichnet. Sie berechnet sich aus dem Quotienten der abgestrahlten Leistung LS und dem Oberflächeninhalt einer Kugel mit dem Radius des mittleren Abstandes zwischen Sonne und Erde (a = 1,5·1011m):
| $$S_0 = \frac{{L_S }}{{4 \cdot \pi \cdot a^2 }} = \frac{{3,87 \cdot 10^{26} W}}{{4 \cdot \pi \cdot \left( {1,5 \cdot 10^{11} m} \right)^2 }} = 1368\frac{W}{{m^2 }}$$ |
(2.4) |
Da die Sonnenstrahlung auf die Projektionsfläche (Wirkungsquerschnitt) der Erde π·rE2 (Erdradius: rE = 6,371·106m) trifft, berechnet sich die auf die Erde eingestrahlte Leistung LE zu:
| $$L_E = S_0 \cdot \pi \cdot r_E^2 \cdot \left( {1 - A} \right)$$ |
(2.5) |
In (2.5) ist berücksichtigt, dass ein Bruchteil A der einfallenden Strahlung, ohne als Energie von der Erde und ihrer Atmosphäre aufgenommen zu werden, direkt in den Weltraum zurückreflektiert wird. A ist die so genannte Albedo.
Unter der Annahme, dass alle auf der Erde eingefallene und absorbierte Energie in Wärme umgewandelt und als Strahlung von der gesamten Erdoberfläche (4·π·rE2) wieder abgegeben wird, muss im stationären Strahlungsgleichgewicht gelten:
| $$4 \cdot \pi \cdot r_E^2 \cdot \sigma \cdot T_E^4 = S_0 \cdot \pi \cdot r_E^2 \cdot \left( {1 - A} \right)$$ |
(2.6) |
Dabei ist TE die Strahlungsgleichgewichtstemperatur der Erde. Nun wird (2.6) nach TE umgestellt:
| $$T_E = \sqrt[4]{{\frac{{S_0 }}{4} \cdot \frac{{1 - A}}{\sigma }}}$$ |
(2.7) |
Da die Erde von der Sonne als Projektionskreisfläche bestrahlt wird, selbst aber eine Kugel ist und das Verhältnis von Kreisfläche zu Kugeloberfläche 1:4 beträgt, wird für die im Mittel von der Erde empfangene Strahlungsenergie die Solarkonstante S0 = 1368W/m2 durch 4 geteilt. Man erhält die bereits in Abbildung 1-1 für die Sonneneinstrahlung angegeben 342W/m2.
Die Albedo berechnet sich aus dem Verhältnis der an den Wolken und am Boden reflektierten Sonnenstrahlung (107W/m2) zur Gesamteinstrahlung der Sonne (342W/m2).
| $$A = \frac{{107\frac{W}{{m^2 }}}}{{342\frac{W}{{m^2 }}}} = 0,313$$ |
(2.8) |
Üblicherweise wird für A in der Literatur ein Wert von 0,3 angegeben. Wir wollen aber in diesem Kapitel den Wert von (2.8) verwenden, da er sich aus den Zahlenangaben aus Abbildung 1-1 ergibt. Damit errechnet sich die Strahlungsgleichgewichtstemperatur der Erde TE zu:
| $$T_E = \sqrt[4]{{342\frac{W}{{m^2 }} \cdot \frac{{1 - 0,313}}{{5,67 \cdot 10^{ - 8} \frac{W}{{m^2 \cdot K^4 }}}}}} = 254K \equiv - 19^\circ C$$ |
(2.9) |
Dieser Wert ist aber deutlich niedriger als die tatsächliche mittlere Temperatur T0 an der Erdoberfläche, denn diese beträgt etwa +15°C. Die Differenz T0 – TE = 34K wird als natürlicher Treibhauseffekt bezeichnet. Üblicherweise wird für TE in der Literatur ein Wert von -18°C angegeben. Wir wollen aber in diesem Kapitel den Wert von (2.9) verwenden, da er sich aus den Zahlenangaben aus Abbildung 1-1 ergibt.
Gegen diese Rechnung kann man einwenden, dass im Albedo von 0,313 nicht nur die hauptsächlich durch Wolken in der Atmosphäre verursachten Reflektionsverluste stecken, sondern auch ein direkt an der Erdoberfläche reflektierter Anteil. In Abbildung 1-1 wird er immerhin mit 30W/m2 angegeben. Auf der anderen Seite wird davon ausgegangen, dass die Erde wie ein schwarzer Körper abstrahlt.
Da der schwarze Körper bei jeder Frequenz das größtmögliche Absorptionsvermögen besitzt, muss er auch bei jeder Frequenz die stärkste physikalisch mögliche thermische Strahlungsleistung wieder abgeben. Jeder andere Körper wird somit bei gleicher Temperatur um den Faktor des Emissionsgrades ε geringer strahlen. Das bedeutet aber im Umkehrschluss, dass bei gleicher Strahlungsleistung der schwarze Körper am kältesten ist. Der Emissionsgrad oder kurz Emission ist das Verhältnis der Strahlungsleistung des realen Körpers zur Strahlungsleistung des idealen schwarzen Körpers und kann Werte zwischen 0 und 1 annehmen (siehe Abbildung 2-1).
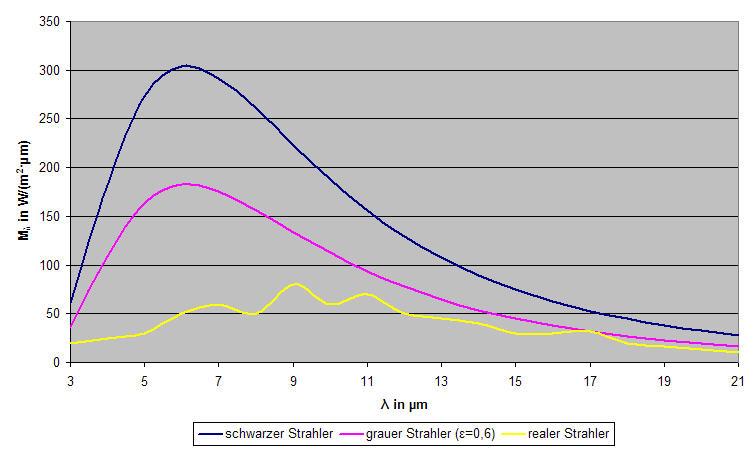
Abb. 2-1: spektrale spezifische Ausstrahlung eines schwarzen, grauen und realen Körpers bei jeweils 473K
So liegt beispielsweise ε für Wasser bei 0,91 und für Sand bei 0,76. Nach Satellitenmessungen liegt εE für die Erde bei 0,8 bis 0,95. Somit sollte (2.6) um εA ≈ 0,9 korrigiert werden:
| $$4 \cdot \pi \cdot r_E^2 \cdot \sigma \cdot T_E^4 \cdot \varepsilon _E = S_0 \cdot \pi \cdot r_E^2 \cdot \left( {1 - A} \right)$$ |
(2.10) |
Gleichung (2.10) nach TE umgestellt und die entsprechenden Werte eingesetzt ergibt:
| $$T_E = \sqrt[4]{{\frac{{S_0 }}{4} \cdot \frac{{1 - A}}{{\sigma \cdot \varepsilon _E }}}} = \sqrt[4]{{342\frac{W}{{m^2 }} \cdot \frac{{1 - 0,313}}{{5,67 \cdot 10^{ - 8} \frac{W}{{m^2 \cdot K^4 }} \cdot 0,9}}}} = 261K \equiv - 12^\circ $$ |
(2.11) |
Die Strahlungsgleichgewichtstemperatur der Erde TE beträgt damit korrigiert -12°C und der natürliche Treibhauseffekt T0 – TE schrumpft auf 26K. Nun wird auch rechnerisch deutlich, wie der Treibhauseffekt funktioniert. Um die Durchschnittstemperatur der Erde nach (2.11) auf die gemessenen +15°C anheben zu können, muss die Emission der Erde entsprechend gesenkt werden. Diese, die Emission senkende Wirkung übernehmen die sogenannten Treibhausgase. Sie absorbieren die Wärmestrahlung in verschiedenen Frequenzbereichen und verhindern daher ihre Abstrahlung in den Weltraum. Zur Beschreibung der Temperaturerhöhung der Erdoberfläche wird der Treibhauseffekt bedingte Emissionsgrad εT eingeführt, der ebenfalls zwischen 0 und 1 liegt. Die mittlere Temperatur der Erdoberfläche T0 berechnet sich dann zu:
| $$T_0 = \sqrt[4]{{\frac{{S_0 }}{4} \cdot \frac{{1 - A}}{{\sigma \cdot \varepsilon _E \cdot \varepsilon _T }}}} = \frac{{T_E }}{{\sqrt[4]{{\varepsilon _T }}}}$$ |
(2.12) |
Um εT genauer bestimmen zu können, sollen wieder die in Abbildung 1-1 gezeigten Energieflüsse zu Hilfe genommen werden. Hier sind die Absorptionseigenschaften der Atmosphäre im Zusammenhang mit der Strahlungsbilanz der Erde dargestellt.
Als Energieeintrag der der Sonne erreichen im Mittel S0/4 = 342W/m2 die Erde. Davon werden 107W/m2 reflektiert (A = Albedo: 77W/m2 durch Wolken und 30W/m2 durch die Erdoberfläche). Weitere 67W/m2 werden in der Atmosphäre absorbiert, vor allem durch O3 und H2O. Den Erdboden erreichen somit 168W/m2. Durch das Verhältnis von tatsächlich empfangener Leistung (168W/m2) zur eingestrahlten nicht reflektierten Leistung (342W/m2 – 107W/m2 = 235W/m2) lässt sich der Transmissionskoeffizient für die kurzwellige Sonnenstrahlung (Licht) τK bestimmen:
| $$\tau _K = \frac{{168\frac{W}{{m^2 }}}}{{235\frac{W}{{m^2 }}}} = 0,715$$ |
(2.13) |
Mit der mittleren Temperatur der Erde T0 = +15°C ≡ 288K lässt sich nach (2.1) die Intensität der resultierenden Wärmestrahlung berechnen (unter stillschweigender Annahme der Erde als schwarzer Strahler):
| $$I_E = \sigma \cdot T_{^0 }^4 = 5,67 \cdot 10^{ - 8} \frac{W}{{m^2 \cdot K^4 }} \cdot \left( {288K} \right)^4 = 390\frac{W}{{m^2 }}$$ |
(2.14) |
Diese 390W/m2 sind auch in Abbildung 1-1 für die Abstrahlung der Erde angegeben. Weitere 24W/m2 werden in Form von konvektivem Wärmefluss und 78W/m2 als latente Wärme (Verdunstungswärme von Wasser), zusammen als ΦH bezeichnet, abgegeben. Der Anteil der direkt ins Weltall abgestrahlten Wärmeleistung wird mit nur 40W/m2 angegeben. Durch das Verhältnis von ungehindert entweichender Leistung (40W/m2) zur von der Erde insgesamt abgestrahlten Leistung (390W/m2) lässt sich der Transmissionskoeffizient für die Wärmestrahlung τA bestimmen:
| $$\tau _A = \frac{{40\frac{W}{{m^2 }}}}{{390\frac{W}{{m^2 }}}} = 0,102$$ |
(2.15) |
Nun wird der Ansatz gemacht, dass die Atmosphäre in beide Richtungen entsprechend einer mittleren Temperatur TA Wärme abstrahlt. Wobei die Atmosphäre nicht als schwarzer Körper betrachtet wird und dementsprechend die Emissionskoeffizienten εA- und εA+ eingefügt werden. Für die Intensität in Richtung Boden IA- wird formuliert:
| $$I_A^ - = \varepsilon _A^ - \cdot \sigma \cdot T_A^4 = 324\frac{W}{{m^2 }}$$ |
(2.16) |
Für die Intensität in Richtung Weltall gilt analog:
| $$I_A^ + = \varepsilon _A^ + \cdot \sigma \cdot T_A^4 = 195\frac{W}{{m^2 }}$$ |
(2.17) |
Wobei allgemein εA- > εA+ gelten soll, da sich die Temperatur mit der Höhe ändert. Bei einer isothermen Atmosphäre würde gelten: εA- = εA+, da der Temperaturgradient dann Null wäre.
Ausgehend von Abbildung 1-1 werden nun zwei Energieflussbilanzen aufgestellt, eine für den oberen Atmosphärenrand und die andere für den Erdboden. Vorausgesetzt wird ein stationäres Strahlungsgleichgewicht, bei dem die Summe der einfallenden gleich der Summe der austretenden Strahlungsleistung ist. Für den oberen Atmosphärenrand gilt also:
| $$\frac{{S_0 }}{4} \cdot \left( {1 - A} \right) = \varepsilon _A^ + \cdot \sigma \cdot T_A^4 + \tau _A \cdot \sigma \cdot T_0^4 $$ |
(2.18) |
Die Bilanz für den Erdboden lautet:
| $$\tau _K \cdot \frac{{S_0 }}{4} \cdot \left( {1 - A} \right) + \varepsilon _A^ - \cdot \sigma \cdot T_A^4 = \Phi _H + \sigma \cdot T_0^4 $$ |
(2.19) |
Aus (2.18) und (2.19) wird nun σ·TA4 eliminiert und es wird nach T0 umgestellt:
| $$\begin{array}{l}
\frac{{\frac{{S_0 }}{4} \cdot \left( {1 - A} \right) - \tau _A \cdot \sigma \cdot T_0^4 }}{{\varepsilon _A^ + }} = \frac{{\Phi _H + \sigma \cdot T_0^4 - \tau _K \cdot \frac{{S_0 }}{4} \cdot \left( {1 - A} \right)}}{{\varepsilon _A^ - }} \\
\frac{{\frac{{S_0 }}{4} \cdot \left( {1 - A} \right)}}{{\varepsilon _A^ + }} - \frac{{\Phi _H - \tau _K \cdot \frac{{S_0 }}{4} \cdot \left( {1 - A} \right)}}{{\varepsilon _A^ - }} = \frac{{\sigma \cdot T_0^4 }}{{\varepsilon _A^ - }} + \frac{{\tau _A \cdot \sigma \cdot T_0^4 }}{{\varepsilon _A^ + }} \\
\frac{{\varepsilon _A^ - }}{{\varepsilon _A^ + }} \cdot \frac{{S_0 }}{4} \cdot \left( {1 - A} \right) - \Phi _H + \tau _K \cdot \frac{{S_0 }}{4} \cdot \left( {1 - A} \right) = \sigma \cdot T_0^4 + \frac{{\varepsilon _A^ - }}{{\varepsilon _A^ + }} \cdot \tau _A \cdot \sigma \cdot T_0^4 \\
\frac{{S_0 }}{4} \cdot \left( {1 - A} \right) \cdot \left( {\frac{{\varepsilon _A^ - }}{{\varepsilon _A^ + }} - \frac{{\Phi _H }}{{\frac{{S_0 }}{4} \cdot \left( {1 - A} \right)}} + \tau _K } \right) = T_0^4 \cdot \sigma \cdot \left( {1 + \frac{{\varepsilon _A^ - }}{{\varepsilon _A^ + }} \cdot \tau _A } \right) \\
T_0^4 = \frac{{\frac{{S_0 }}{4} \cdot \left( {1 - A} \right)}}{\sigma } \cdot \frac{{\frac{{\varepsilon _A^ - }}{{\varepsilon _A^ + }} - \frac{{\Phi _H }}{{\frac{{S_0 }}{4} \cdot \left( {1 - A} \right)}} + \tau _K }}{{1 + \frac{{\varepsilon _A^ - }}{{\varepsilon _A^ + }} \cdot \tau _A }} \\
\end{array}$$ |
|
| $$T_0 = \sqrt[4]{{\frac{{S_0 }}{4} \cdot \frac{{1 - A}}{\sigma }}} \cdot \sqrt[4]{{\frac{{\frac{{\varepsilon _A^ - }}{{\varepsilon _A^ + }} - \frac{{\Phi _H }}{{\frac{{S_0 }}{4} \cdot \left( {1 - A} \right)}} + \tau _K }}{{1 + \frac{{\varepsilon _A^ - }}{{\varepsilon _A^ + }} \cdot \tau _A }}}}$$ |
(2.20) |
Die erste Wurzel ergibt nach (2.7) die Strahlungsgleichgewichtstemperatur der Erde TE. Des Weiteren wird das Verhältnis εA-/εA+ durch ε~ ersetzt:
| $$T_0 = T_E \cdot \sqrt[4]{{\frac{{\tilde \varepsilon - \frac{{\Phi _H }}{{\frac{{S_0 }}{4} \cdot \left( {1 - A} \right)}} + \tau _K }}{{1 + \tilde \varepsilon \cdot \tau _A }}}} = T_E \cdot \sqrt[4]{{\frac{{\tilde \varepsilon - \tau _K \cdot \frac{{\Phi _H }}{{\tau _K \cdot \frac{{S_0 }}{4} \cdot \left( {1 - A} \right)}} + \tau _K }}{{1 + \tilde \varepsilon \cdot \tau _A }}}}$$ |
|
| $$T_0 = T_E \cdot \sqrt[4]{{\frac{{\tilde \varepsilon + \tau _K \cdot \left( {1 - \frac{{\Phi _H }}{{\tau _K \cdot \frac{{S_0 }}{4} \cdot \left( {1 - A} \right)}}} \right)}}{{1 + \tilde \varepsilon \cdot \tau _A }}}} = T_E \cdot \sqrt[4]{{\frac{{\tilde \varepsilon + \tau _K \cdot \left( {1 - \alpha } \right)}}{{1 + \tilde \varepsilon \cdot \tau _A }}}}$$ |
(2.21) |
Der Parameter α ist das Verhältnis des latenten Wärmeflusses ΦH (in Abbildung 1-1 mit 102W/m2 angegeben) zur tatsächlich am Boden absorbierten Sonnenstrahlung (in Abbildung 1-1 mit 168W/m2 angegeben). Somit lässt sich α wie folgt bestimmen:
| $$\alpha = \frac{{\Phi _H }}{{\tau _K \cdot \frac{{S_0 }}{4} \cdot \left( {1 - A} \right)}} = \frac{{102\frac{W}{{m^2 }}}}{{168\frac{W}{{m^2 }}}} = 0,607$$ |
(2.22) |
Der Parameter ε~ berechnet sich aus den Angaben aus Abbildung 1-1 und (2.16), (2.17) zu:
| $$\tilde \varepsilon = \frac{{\varepsilon _A^ - }}{{\varepsilon _A^ + }} = \frac{{324\frac{W}{{m^2 }}}}{{195\frac{W}{{m^2 }}}} = 1,662$$ |
(2.23) |
Nach (2.12) kann jetzt (2.21) auch geschrieben werden (wobei hier εE = 1 gesetzt wird):
| $$T_0 = \frac{{T_E }}{{\sqrt[4]{{\varepsilon _T }}}} = \frac{{T_E }}{{\sqrt[4]{{\frac{{1 + \tilde \varepsilon \cdot \tau _A }}{{\tilde \varepsilon + \tau _K \cdot \left( {1 - \alpha } \right)}}}}}}$$ |
(2.24) |
Mit (2.13), (2.15), (2.22) und (2.23) lässt sich nun εT entsprechend den Angaben aus Abbildung 1-1 berechnen:
| $$\varepsilon _T = \frac{{1 + \tilde \varepsilon \cdot \tau _A }}{{\tilde \varepsilon + \tau _K \cdot \left( {1 - \alpha } \right)}} = \frac{{1 + \left( {1,662 \cdot 0,102} \right)}}{{1,662 + 0,715 \cdot \left( {1 - 0,607} \right)}} = 0,602$$ |
(2.25) |
Da alle Angaben aus Abbildung 1-1 abgeleitet wurden, und eine mittlere Temperatur der Erdoberfläche von +15°C den gesamten Berechnungen zugrunde liegt, muss (2.25) mit dem berechneten Wert für εT auch wieder +15°C ergeben:
| $$T_0 = \frac{{254K}}{{\sqrt[4]{{0,602}}}} = 288K \equiv + 15^\circ C$$ |
(2.26) |
Zur Erscheinungszeit von "Chemie und Umwelt" war man noch der Auffassung, dass durch eine Erhöhung der Konzentration des Spurengases CO2 und der damit verbundenen Absenkung des Transmissionskoeffizienten der Wärmestrahlung τA sich eine wesentliche Temperaturerhöhung ableiten ließl;e. Genau das ist die Stelle, an der eine Erhöhung der Spurengaskonzentration angreifen kann. Seine Definition lautet folgendermaßl;en:
| $$\tau _A = e^{ - \int\limits_0^\infty {\kappa \cdot \rho (h) \cdot dh} } $$ |
(2.27) |
Die Gleichung (2.27) leitet sich aus dem Lambert-Beerschen-Gesetz ab, auf das später noch eingegangen wird. Das Symbol κ bezeichnet den effektiven Absorptionskoeffizienten. Er beschreibt die Absorptionsfähigkeit eines durchstrahlten Mediums unabhängig seiner Dichte bzw. Konzentration und ist somit rein materialabhängig. ρ(h) ist die Dichte bzw. Konzentration des Mediums. Da das Medium in unserem Fall die Atmosphäre ist, nimmt die Dichte mit der Höhe h ab. Daher steht in der e-Funktion auch das Integral als Exponent. Es wird bestimmt über seine Grenzen, wobei die Grenze 0 der Erboden ist und ∞ der obere noch mit Materie gefüllte Atmosphärenrand.
Das Lambert-Beerschen-Gesetz gilt genau genommen nur für einen monochromatischen Strahl, also nur für eine Wellenlänge, da der Absorptionskoeffizient κ wellenlängenabhängig ist. Jede Molekülart absorbiert aber auch nur in den für sie typischen Wellenlängenbereichen. Trotzdem wurde in der Klimamodellierung von "geeigneten Mittelwerten" ausgegangen, um mit (2.27) rechnen zu können.
Nach (2.15) ist aber τA mit 0,102 bereits ziemlich klein, so dass das klimawirksame Potential analog zum Kapitel 1 nicht sehr hoch erscheint. Nach Abbildung 1-1 werden nur 40W/m2 direkt (ohne vorherige Absorption) in das Weltall abgestrahlt. Und nur diese Intensität steht für einen zusätzlichen Treibhauseffekt zur Verfügung.
Es wurde daher argumentiert, dass die Parameter aus (2.24) nicht voneinander unabhängig sind. So hängen εA- und εA+ von τA ab, da sich die vom Modell beschriebene atmosphärische Wärmestrahlung aus der vorher absorbierten Wärmeenergie speisen muss. Eine Absenkung von τA soll daher zu einer Erhöhung von εA- und εA+ führen, wobei durch den Temperaturgradienten in der Atmosphäre eine Veränderung des Verhältnisses zwischen εA- und εA+ bewirkt wird. Der Parameter α hängt nach (2.22) von τK ab. Da τK die Absorption der kurzwelligen Strahlung (Licht) in der Atmosphäre durch Ozon und Wasserdampf beschreibt (wodurch es ebenfalls zu einer Erwärmung der Atmosphäre kommt), sind εA- und εA+ auch von τK abhängig. Da CO2 aber auch Absorptionsbande im Bereich des Lichts besitzt, wird τK bei Erhöhung der CO2-Konzentration sinken, was letztendlich zu einem dämpfenden Effekt auf den Anstieg der Erdtemperatur führen dürfte. Man bekommt aber einen Eindruck, wie man mit diesen Parametern trefflich jonglieren kann, ohne genau zu wissen, ob man alle Abhängigkeiten korrekt abbildet.
Als Beispiel dafür, wie vermutlich logisch schlüssige Daten aus falschen Voraussetzungen modelliert werden, mag Tabelle 2-1 dienen, die ebenfalls aus "Chemie und Umwelt" (Reinhardt/Heintz, Vieweg & Sohn Verlagsgesellschaft mbH, Braunschweig, 1990, S.42) stammt. Hier wird erklärt, wie viel Grad jedes Spurengas ausgehend von seiner derzeitigen Konzentration in der Atmosphäre zum Treibhauseffekt von ∑iΔTi = 33K beiträgt. Startpunkt der "detaillierten Modellrechnung" ist die Strahlungsgleichgewichtstemperatur der Erde TE = -18°C. Darüber, dass sich nach (2.9) eine Strahlungsgleichgewichtstemperatur der Erde von -19°C ergibt, wollen wir hier nicht streiten.
| Temperaturbeitrag |
H2O-Dampf |
CO2 |
O3 (Trop.) |
N2O |
CH4 |
Rest |
| ΔTi in K |
20,6 |
7,2 |
2,4 |
1,4 |
0,8 |
0,6 |
| ΔTi in % |
62,4 |
21,8 |
7,3 |
4,3 |
2,4 |
1,8 |
Tab. 2-1: Anteile der einzelnen Spurengase am natürlichen Treibhauseffekt nach "Chemie und Umwelt" (S.42)
Bei der Modellrechnung wird ganz selbstverständlich von der Erde als ideal schwarzen Körper ausgegangen, die sie aber nach (2.11) real nicht ist. So kann durch Variation und Anpassung nahezu jedes gewünschte Ergebnis modelliert werden. Mit der Realität hat das sicher wenig zu tun.
Zum Vergleich wurden in Tabelle 2-2 die Berechnungen mit den Angaben für die Strahlungsbilanz aus "Chemie und Umwelt" (Reinhardt/Heintz, Vieweg & Sohn Verlagsgesellschaft mbH, Braunschweig, 1990, S.39) wiederholt und mit denen aus Abbildung 1-1 gegenübergestellt. In den letzten vier Tabellenzeilen sind die Parameter τK, τA, ε~ und α aufgeführt. Hier fällt auf, dass zwischen beiden Ansätzen zum Teil erhebliche Unterschiede bestehen, obwohl die Gesamtenergiebilanz immer stimmt. Es scheint aber schwierig zu sein, sich auf mittlere Energieströme überhaupt festlegen zu können. Der größte Unterschied liegt in dem Energieanteil, der ohne Absorption in der Atmosphäre direkt von der Erdoberfläche abgestrahlt wird τA·σ·T04 und damit auch in dem Parameter τA.
| - |
Wikipedia (Abb. 1-1) |
"Chemie und Umwelt" |
| S0/4 |
342W/m2 |
342W/m2 |
| S0/4 · A |
107W/m2 |
103W/m2 |
| τK · S0/4 · (1-A) |
168W/m2 |
154W/m2 |
| ε+ · σ · TA4 |
195W/m2 |
226W/m2 |
| ε- · σ · TA4 |
324W/m2 |
328W/m2 |
| σ · T04 |
390W/m2 |
383W/m2 |
| τA · σ · T04 |
40W/m2 |
14W/m2 |
| ΦH |
102W/m2 |
99W/m2 |
| τK |
0,715 |
0,643 |
| τA |
0,102 |
0,036 |
| α |
0,607 |
0,644 |
| ε~ |
1,662 |
1,455 |
Tab. 2-2: Energieflüsse der Erde nach Wikipedia und "Chemie und Umwelt" (S.39)
Die Atmosphäre besteht hauptsächlich aus den zwei Gasen Stickstoff (78%) und Sauerstoff (21%). Daneben gibt es noch das Edelgas Argon (0,9%), Kohlenstoffdioxid (0,038%) und in Spuren Wasserdampf.Nach Tabelle 2-1 ist CO2 nach Wasserdampf das hauptverantwortliche Spurengas für den Treibhauseffekt. Da Wasserdampf natürlicherweise immer auftritt und seine Konzentration stark schwankt, wird er nicht als Klimakiller angesehen. Das Augenmerk liegt zum größten Teil auf dem Spurengas Kohlendioxid. Da dieses hauptsächliche Stoffwechselendprodukt unserer Industrie und unserer Lebensweise unserem Planeten am meisten einheizen soll, werden wir uns im weiteren Verlauf dieser Abhandlung im Wesentlichen auf dieses Molekül konzentrieren.
Die Strahlungsgleichgewichtstemperatur der Erde nach (2.9) ist immer unter Berücksichtigung des durch Wolken verursachten Albedos berechnet. Denken wir uns dagegen das Wasser auf der Erde und auch die Atmosphäre weg, so müssen wir nur noch die Reflektionen am Erdboden berücksichtigen. Die Albedos AW nach Wikipedia (Abbildung 1-1) und ACuU nach "Chemie und Umwelt" (Reinhardt/Heintz, Vieweg & Sohn Verlagsgesellschaft mbH, Braunschweig, 1990, S.39, rE = relative Einheit) schrumpfen dann auf:
| $$A_W = \frac{{30\frac{W}{{m^2 }}}}{{196\frac{W}{{m^2 }}}} = 0,153$$ |
(2.28) |
| $$A_{CuU} = \frac{4rE}{{49rE}} = 0,0816$$ |
(2.29) |
Damit ergeben sich analog (2.11) folgende neue Strahlungsgleichgewichtstemperaturen der Erde:
| $$T_{EW} = \sqrt[4]{{342\frac{W}{{m^2 }} \cdot \frac{{1 - 0,153}}{{5,67 \cdot 10^{ - 8} \frac{W}{{m^2 \cdot K^4 }} \cdot 0,9}}}} = 274,5K \equiv 1,5^\circ C$$ |
(2.30) |
| $$T_{ECuU} = \sqrt[4]{{342\frac{W}{{m^2 }} \cdot \frac{{1 - 0,0816}}{{5,67 \cdot 10^{ - 8} \frac{W}{{m^2 \cdot K^4 }} \cdot 0,9}}}} = 280,1K \equiv 7,1^\circ C$$ |
(2.31) |
Nach dieser Rechnung muss (insgesamt gesehen) das Potential der klimawirksamen Gase wesentlich kleiner sein, als in Tabelle 2-1 angegeben worden ist.
|

