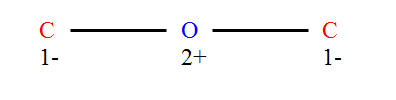|
|
Jeder feste oder flüssige Körper strahlt entsprechend seiner Temperatur in einem kontinuierlichen Spektrum Wärmestrahlung aus. Die Verteilung dieser Wärmestrahlung im Frequenzbereich (Spektrum) erfolgt nach dem Planckschen Strahlungsgesetz und wird mittels der spezifischen spektralen Ausstrahlung Mf0(f, T) in der Einheit W/(m2·Hz) angegeben:
| $$M_f^0 \left( {f,T} \right) \cdot dA \cdot df = \frac{{2 \cdot \pi \cdot h \cdot f^3 }}{{c^2 }} \cdot \frac{1}{{e^{\frac{{h \cdot f}}{{k_B \cdot T}}} - 1}} \cdot dA \cdot df$$ |
(5.1) |
Die spezifische spektrale Ausstrahlung gibt an wie viel Energie durch das Flächenelement dA im Frequenzbereich f+df bei der Temperatur T abgestrahlt wird. Die übrigen Parameter sind bekannt: h ist wieder das Plancksche Wirkungsquantum, kB die Boltzmann-Konstante und c die Lichtgeschwindigkeit. Wird (5.1) über die Frequenz integriert, so erhält man das Stefan-Boltzmann-Gesetz nach (2.1).
| $$\int\limits_0^\infty {M_f^0 \left( {f,T} \right) \cdot df} = \int\limits_0^\infty {\frac{{2 \cdot \pi \cdot h \cdot f^3 }}{{c^2 }} \cdot \frac{1}{{e^{\frac{{h \cdot f}}{{k_B \cdot T}}} - 1}} \cdot df} = \sigma \cdot T^4 $$ |
(5.2) |
Man kann (5.1) auch über die Wellenlänge λ ausdrücken. Mit f = c/λ wird aus (5.1):
| $$M_\lambda ^0 \left( {\lambda ,T} \right) \cdot dA \cdot d\lambda = \frac{{2 \cdot \pi \cdot h \cdot c}}{{\lambda ^3 }} \cdot \frac{1}{{e^{\frac{{h \cdot c}}{{\lambda \cdot k_B \cdot T}}} - 1}} \cdot dA \cdot df$$ |
|
Nun wird df durch dλ substituiert:
| $$f = \frac{c}{\lambda }$$ |
→ |
$$\frac{{df}}{{d\lambda }} = - \frac{c}{{\lambda ^2 }}$$ |
→ |
$$\left| {df} \right| = \left| { - \frac{c}{{\lambda ^2 }} \cdot d\lambda } \right|$$ |
|
| $$M_\lambda ^0 \left( {\lambda ,T} \right) \cdot dA \cdot d\lambda = \frac{{2 \cdot \pi \cdot h \cdot c^2 }}{{\lambda ^5 }} \cdot \frac{1}{{e^{\frac{{h \cdot c}}{{\lambda \cdot k_B \cdot T}}} - 1}} \cdot dA \cdot d\lambda $$ |
(5.3) |
Abbildung 5-1 zeigt Plancksche Strahlungsspektren für verschiedene Temperaturen zwischen 100K und 10000K in doppelt logarithmischer Darstellung. Die Kurven haben ein deutlich ausgeprägtes Strahlungsmaximum, einen steilen Abfall hin zu kurzen Wellenlängen und einem länger auslaufenden Abfall hin zu großen Wellenlängen. Die Lage des Strahlungsmaximums verschiebt sich mit zunehmender Temperatur zu kürzeren Wellenlängen. Die Fläche unter der jeweiligen Kurve für die spektrale spezifische Ausstrahlung entspricht der gesamten spezifischen Ausstrahlung. Sie nimmt nach (5.2), dem Stefan-Boltzmann-Gesetz, mit der vierten Potenz der absoluten Temperatur zu.
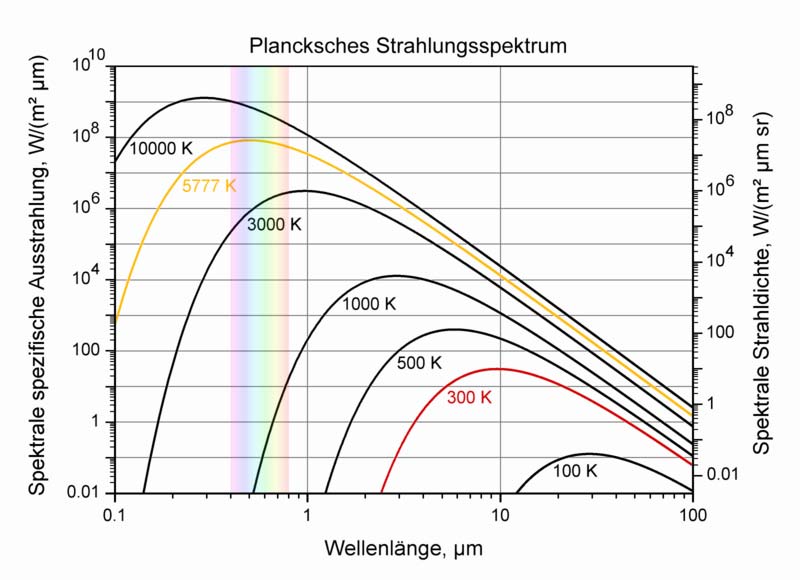
Abb. 5-1: Plancksche Strahlungsspektren für verschiedene Temperaturen in doppeltlogarithmischer Auftragung (Quelle: Wikipedia Plancksches Strahlungsgesetz)
Die rot hervorgehobene Kurve von 300K stellt eine mögliche Oberflächentemperatur der Erde dar. Das Maximum dieser Kurve liegt bei 10μm, was ca. 30THz entspricht. In diesem Frequenzbereich finden Schwingungsvorgänge in Molekülen statt. Die Treibhausgase müssen daher auch in diesem Bereich infrarotaktiv sein, damit es überhaupt zu einem Treibhauseffekt kommen kann. Jeglicher Strahlungsaustausch von Objekten auf Raumtemperatur läuft in diesem Frequenzbereich ab.
Die 3000K-Kurve ist das Strahlungsspektrum einer Glühlampe. Ein Teil der emittierten Strahlung wird im schematisch angedeuteten sichtbaren Spektralbereich abgegeben, wobei sich das Strahlungsmaximum im nahen Infrarot befindet.
Die gelbe Kurve zeigt das Strahlungsspektrum der Sonne bei einer Effektivtemperatur von 5777K. Das Strahlungsmaximum liegt genialer Weise mitten im sichtbaren Spektralbereich, wobei die thermisch ausgestrahlte kurzwellige UV-Strahlung zum größten Teil von der Ozonschicht der Erdatmosphäre ausgefiltert wird.
Im Molekül sind mehrere Atome in definierter räumlicher Lage relativ zueinander angeordnet. Die Abstände der Atomkerne werden durch die Summe aller zwischen den Atomkernen und den Elektronen wirkenden Kräften festgelegt. Diese Bindungskräfte wirken wie eine masselose Feder an deren Enden sich die Massen der Atomkerne befinden. Man erhält auf diese Weise ein schwingfähiges Masse-Feder-System. Abbildung 5-2 zeigt die Streckschwingung des homonuklearen zweiatomigen Sauerstoffmoleküls um den Gleichgewichtsabstand Re. Um die Schwingung zu verstehen, soll zunächst dieser einfache Fall betrachtet werden.
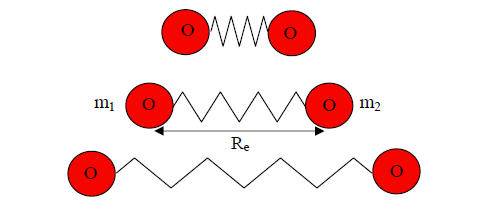
Abb. 5-2: Streckschwingung von O2 um den Gleichgewichtsabstand Re
Wird ein solches Molekül von einem anderen Molekül mit der nötigen Geschwindigkeit in Richtung der Bindungsachse getroffen, so wird nach dem Impulserhaltungssatz ein Teil der Bewegungsenergie stoßenden Moleküls auf den getroffenen Atomkern übertragen. Dieser wird beschleunigt und es kommt zu einer Stauchung des gestoßenen Moleküls. Damit wird aber durch die gespannte Feder eine Rückstellkraft erzeugt, die die Atomkerne zwingt, sich wieder voneinander weg zu bewegen. Es entsteht eine Schwingung um den Gleichgewichtsabstand Re. Das stoßende Molekül wird dabei abgebremst. Genau wie bei der Rotation hat ein schwingfähiges System mehr innere Freiheitsgrade und damit eine höhere Wärmekapazität als ein nicht schwingfähiges System.
Um dieses System einfacher berechnen zu können, wird die reduzierte Masse eingeführt. Man stellt sich modellhaft vor, dass nur ein Teilchen mit der Masse mr mit Hilfe einer an einer Wand befestigten Feder um Re schwingt. Die reduzierte Masse berechnet sich wie folgt:
| $$m_r = \frac{{m_1 \cdot m_2 }}{{m_1 + m_2 }}$$ |
(5.4) |
In Abbildung 5-3 ist das beschriebene Rechenmodell abgebildet. Wird die reduzierte Masse für ein homonukleares Molekül wie z.B. O2 nach (5.4) berechnet, so erhält man die Hälfte der Masse eines Atoms als Ergebnis.
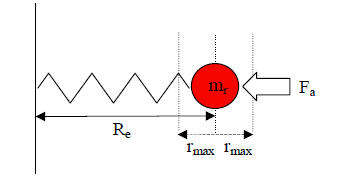
Abb. 5-3: Schwingung der reduzierten Masse mr
Durch den Stoß wird der Impuls p = mr·v übertragen. Oder anders ausgedrückt die Masse mr erfährt die Beschleunigung a. Die wirkende Beschleunigungskraft Fa berechnet sich zu:
| $$F_a = \frac{{dp}}{{dt}} = m_r \cdot \frac{{dv}}{{dt}} = m_r \cdot \frac{{d^2 r}}{{dt^2 }} = m_r \cdot a$$ |
(5.5) |
Die durch die Stauchung um r entstehende Rückstellkraft FR wird mit Hilfe der Federkonstanten k wie folgt berechnet:
| $$F_R = k \cdot r$$ |
(5.6) |
Da der Vorgang durch einen kurzen Impuls ausgelöst wurde, entsteht folgendes Kräftegleichgewicht:
| $$F_a + F_R = 0$$ |
→ |
$$m_r \cdot \frac{{d^2 r}}{{dt^2 }} + k \cdot r = 0$$ |
(5.7) |
Die homogene Differentialgleichung 2. Ordnung (5.7) beschreibt eine ungedämpfte harmonische Schwingung, aus der man die Kreisfrequenz ω0 = 2·π·f0 sofort angeben kann:
| $$\frac{{m_r }}{k} \cdot \frac{{d^2 r}}{{dt^2 }} + r = \frac{1}{{\omega _0^2 }} \cdot \frac{{d^2 r}}{{dt^2 }} + r = 0$$ |
(5.8) |
| $$\omega _0 = \sqrt {\frac{k}{{m_r }}} $$ |
(5.9) |
Damit beträgt die Resonanzfrequenz des Feder-Masse-Systems:
| $$f_0 = \frac{1}{{2 \cdot \pi }} \cdot \sqrt {\frac{k}{{m_r }}} $$ |
(5.10) |
Um sich eine Vorstellung über die Größe der Federkonstanten k machen zu können, sind in Tabelle 5-1 typische Federkonstanten abhängig von ihren molekülspezifischen Bindungsarten angegeben. Verwendet wurde das Buch "Molekülphysik und Quantenchemie" (Haken/Wolf, Springer-Verlag, Heidelberg, 1991, S.161).
| kovalente Bindung z.B. H2 |
Doppelbindung z.B. O2 |
Dreifachbindung z.B. N2 |
Ionenbindung z.B. NaCl |
| k = 520N/m |
k = 1140N/m |
k = 2260N/m |
k = 120N/m |
Tab. 5-1: typische Federkonstanten für verschiedene Bindungsarten
Als nächstes soll die Bewegungsgleichung der Schwingung hergeleitet werden, die die homogene Differentialgleichung (5.8) erfüllt. Dazu wird (5.8) zuerst etwas umgestellt:
| $$\frac{{d^2 r}}{{dt^2 }} = \frac{{d\left( {\frac{{dr}}{{dt}}} \right)}}{{dt}} = - \omega _0^2 \cdot r$$ |
→ |
$$d\left( {\frac{{dr}}{{dt}}} \right) = - \omega _0^2 \cdot r \cdot dt$$ |
|
Nun werden beide Seiten integriert, wobei die Integrationskonstante auf 0 gesetzt wird, da das System sich vor dem Stoß in Ruhe befand.
| $$\int {d\left( {\frac{{dr}}{{dt}}} \right)} = - \omega _0^2 \cdot \int {r \cdot dt} $$ |
→ |
$$\frac{{dr}}{{dt}} = - \omega _0^2 \cdot r \cdot t$$ |
→ |
$$\frac{{dr}}{r} = - \omega _0^2 \cdot t \cdot dt$$ |
|
Erneut werden beide Seiten integriert, wobei diesmal die Integrationskonstante c benötigt wird:
| $$\int {\frac{{dr}}{r}} = - \omega _0^2 \cdot \int {t \cdot dt} $$ |
→ |
$$\ln r + c = - \omega _0^2 \cdot \frac{1}{2} \cdot t^2 $$ |
|
Die Konstante c kann aber als Logarithmus einer weiteren Konstanten aufgefasst werden, die der Einfachheit halber wieder mit c bezeichnet werden soll. Nach den Logarithmusgesetzen wird aus einer Addition eine Multiplikation. Daher gilt:
| $$\ln \left( {c \cdot r} \right) = - \omega _0^2 \cdot \frac{1}{2} \cdot t^2 $$ |
→ |
$$2 \cdot \ln \left( {c \cdot r} \right) = - \omega _0^2 \cdot t^2 $$ |
|
Nun wird auf beiden Seiten die Wurzel gezogen. Da die rechte Seite negativ ist, entsteht eine komplexe Zahl.
| $$\left( {2 \cdot \ln \left( {c \cdot r} \right)} \right)^{\frac{1}{2}} = j \cdot \omega _0 \cdot t$$ |
|
Beide Seiten werden in eine Exponentialfunktion überführt, wobei nach den Gesetzen der Potenzfunktion die Exponenten multipliziert werden:
| $$e^{\left( {2 \cdot \ln \left( {c \cdot r} \right)} \right)^{\frac{1}{2}} } = e^{j \cdot \omega _0 \cdot t} $$ |
→ |
$$e^{\frac{1}{2} \cdot 2 \cdot \ln \left( {c \cdot r} \right)} = e^{\ln \left( {c \cdot r} \right)} = c \cdot r = e^{j \cdot \omega _0 \cdot t} $$ |
|
Umgestellt nach r und die Konstante c angepasst ergibt sich:
| $$r = c \cdot e^{j \cdot \omega _0 \cdot t} $$ |
|
Da es bei einem ungedämpft schwingendem System egal ist, an welche Stelle der Anfang t = 0 gelegt wird, so soll er zweckmäßig auf den Zustand maximaler Auslenkung r = rmax gelegt werden. Somit kann c für t = 0 auf rmax bestimmt werden. Schwingungstechnisch beschreibt rmax die Amplitude der Schwingung und ω0 ihre Kreisfrequenz.
| $$r = r_{\max } \cdot e^{j \cdot \omega _0 \cdot t} $$ |
|
Die e-Funktion mit j im Exponenten wird auch als Einheitsdrehvektor bezeichnet. Er hat in der Gaußschen Zahlenebene den Betrag 1 und die Winkelgeschwindigkeit ω0. Eine komplexe Zahl dieser Form wird auch als Exponentialform bezeichnet und kann leicht in die trigonometrische Form mit einem Real- und Imaginärteil zerlegt werden:
| $$r = r_{\max } \cdot \left( {\cos \omega _0 t + j\sin \omega _0 t} \right)$$ |
|
Die Projektion auf die reale Achse der Gaußschen Zahlenebene ist die Lösung von (5.8). Damit entsteht für das Feder-Masse-System eine harmonische Schwingung mit der Kreisfrequenz ω0 und der Amplitude rmax.
| $$r = r_{\max } \cdot \cos \omega _0 t$$ |
(5.11) |
Aus (5.6) kann die Formel für die potentielle Energie Evib des schwingenden Systems durch Integration gewonnen werden:
| $$E_{vib} = \int {F_R \cdot dr} = k \cdot \int {r \cdot dr} = \frac{1}{2} \cdot k \cdot r^2 $$ |
(5.12) |
Als nächstes sollen die Eigenfrequenzen der Streckschwingungen für das O2- und das N2-Molekül berechnet werden. Dazu werden als Voraussetzung die reduzierten Massen benötigt. Wegen m1 = m2 ist die reduzierte Masse nach (5.4) gleich der Hälfte der Masse eines Atoms.
| $$m_{Or} = \frac{{16 \cdot u}}{2} = 8 \cdot 1,6606 \cdot 10^{ - 27} kg = 1,328 \cdot 10^{ - 26} kg $$ |
$$m_{Nr} = \frac{{14 \cdot u}}{2} = 7 \cdot 1,6606 \cdot 10^{ - 27} kg = 1,162 \cdot 10^{ - 26} kg$$ |
|
Mit den Federkonstanten nach Tabelle 5-1 lassen sich nach (5.10) die Eigenfrequenzen und die zugehörigen Wellenlängen berechnen.
| $$f_{O_2 } = \frac{1}{{2 \cdot \pi }} \cdot \sqrt {\frac{{1140\frac{N}{m}}}{{1,328 \cdot 10^{ - 26} kg}}} = 46,63THz$$ |
→ |
$$\lambda _{O_2 } = \frac{c}{{f_{O_2 } }} = \frac{{300000000\frac{m}{s}}}{{46,63THz}} = 643,3nm$$ |
|
| $$f_{N_2 } = \frac{1}{{2 \cdot \pi }} \cdot \sqrt {\frac{{2260\frac{N}{m}}}{{1,162 \cdot 10^{ - 26} kg}}} = 70,19THz$$ |
→ |
$$\lambda _{N_2 } = \frac{c}{{f_{N_2 } }} = \frac{{300000000\frac{m}{s}}}{{70,19THz}} = 427,4nm$$ |
|
Da Moleküle Schwingungsenergie genau wie Rotationsenergie nur in diskreten Energiesprüngen (Quanten) aufnehmen können, kann (5.12) nicht direkt zur Berechnung der Schwingungsenergie verwendet werden. Nach dem Buch "Molekülphysik und Quantenchemie" (Haken/Wolf, Springer-Verlag, Heidelberg, 1991, S.155) lautet die Quantenbeziehung für die Energieeigenwerte der Schwingung:
| $$E_{vib} = h \cdot f_0 \cdot \left( {V + \frac{1}{2}} \right)$$ |
$$V = 0,1,2,3,...$$ |
(5.13) |
Dabei ist h = 6,6261·10-34Js das bereits bekannte Plancksche Wirkungsquantum und V die Schwingungsquantenzahl, mit der die einzelnen diskreten Schwingungsniveaus durchnummeriert werden. In (5.13) fällt auf, dass die Energie für den nicht angeregten Grundzustand V = 0 größer als Null ist. Sie berechnet sich zu:
| $$E_{vib} \left( {V = 0} \right) = \frac{{h \cdot f_0 }}{2}$$ |
(5.14) |
Als nächstes soll berechnet werden, welche Energie notwendig ist, um die Schwingung von einem Zustand V auf den folgenden Zustand V+1 zu erhöhen. Dazu müssen die Schwingungsenergien zweier aufeinander folgender Zustände voneinander subtrahiert werden:
| $$E_{V + 1} - E_V = f_0 \cdot h \cdot \left( {V + 1,5} \right) - f_0 \cdot h \cdot \left( {V + 0,5} \right) = f_0 \cdot h$$ |
(5.15) |
Die Abstände zwischen zwei aufeinander folgenden Energieniveaus EV und EV+1 bleiben im Gegensatz zur Rotation bei jedem übergang gleich – sie sind äquidistant. Daher muss bei jedem Übergang auf ein höheres Schwingungsniveau die gleiche Energie aufgewendet werden, wie beim vorherigen Übergang. Folgerichtig sieht man in Schwingungsspektren im Gegensatz zu Rotationsspektren nur eine Linie bei der Eigenfrequenz f0 und keine Bande von Spektrallinien.
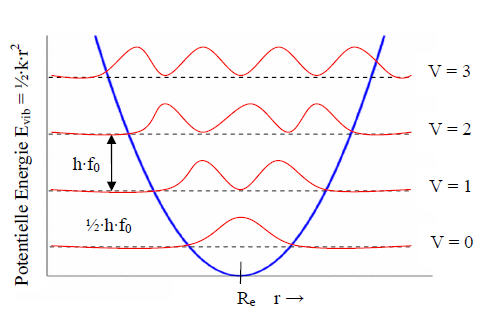
Abb. 5-4: Potentialkurve mit Energieniveaus des harmonischen Oszillators
Die Abbildung 5-4 zeigt die parabelförmige potentielle Energie nach (5.12) in Abhängigkeit der Auslenkung r. Die gequantelte Struktur der Energieniveaus wird dadurch anschaulich, dass nur ganzzahlige Vielfache der Eigenfrequenz f0 in das vorgegebene Energieniveau passen. Wobei für jedes Niveau noch die immer vorhandene Nullpunktenergie nach (5.14) hinzugezählt werden muss, die sogar bei 0K vorhanden ist und daher auch nicht unterschritten werden kann.
Bisher wurden nur zweiatomige Moleküle betrachtet. Bei mehratomigen Molekülen sind entsprechend mehr Schwingungsformen möglich. In Abbildung 5-5 sind die möglichen Schwingungsformen von dreiatomigen linearen und nichtlinearen Molekülen dargestellt.
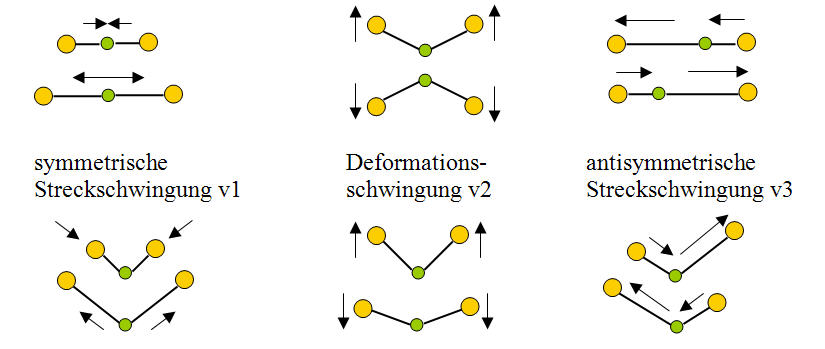
Abb. 5-5: Schwingungsformen dreiatomiger Moleküle (oben CO2, unten H2O)
Das CO2-Molekül kann:
| 1) |
die symmetrische Streckschwingung v1 vollführen, wobei sich beide Sauerstoffatomkerne linear und symmetrisch vom Kohlenstoffatomkern weg und auf ihn zu bewegen (Diese Schwingung hat die Frequenz fv1 = 38,55THz.) |
| 2) |
die Deformationsschwingung v2 vollführen, wobei sich der Kohlenstoffatomkern so zwischen den Sauerstoffatomkernen bewegt, dass er die Linie verlässt (Diese Schwingung kann einmal in der Ebene erfolgen und einmal senkrecht dazu. Beide Schwingungen sind völlig gleichwertig, werden aber durch unterschiedliche Raumkoordinaten beschrieben. Man nennt diese Schwingung daher zweifach entartet. Sie hat die Frequenz fv2 = 20,01THz.) |
| 3) |
die asymmetrische Streckschwingung vollführen, wobei sich der Kohlenstoffatomkern linear so bewegt, dass sich in einer Halbwelle der Abstand zu einem Sauerstoffatomkern verkürzt und zum anderen verlängert (In der zweiten Halbwelle kehrt sich diese Situation entsprechend um. Diese Schwingung hat die Frequenz fv3 = 70,47THz.) |
Die Frequenz der Deformationsschwingung ist am niedrigsten, was darauf hindeutet, dass die Federkonstante bei dieser Schwingungsart am geringsten ist. Die Bindungskräfte werden hier am wenigsten belastet.
Molekülschwingungen können durch Stöße mit anderen Molekülen angeregt werden, die allerdings die dazu nötige Bewegungsenergie besitzen müssen. Auf der anderen Seite kann ein schwingendes Molekül diese Schwingungsenergie durch Stöße auf ein anderes Molekül wieder abgeben und dieses dabei beschleunigen. Im Mittel wird sich ein Gleichgewicht zwischen der Anzahl der schwingenden zur Anzahl der nichtschwingenden Moleküle einstellen. Das Verhältnis hängt von der Temperatur ab und wird durch die Boltzmann-Statistik beschrieben:
| $$\frac{{N_1 }}{{N_0 }} \propto e^{ - \frac{{E_1 - E_0 }}{{k_B \cdot T}}} = e^{ - \frac{{h \cdot f_0 }}{{k_B \cdot T}}} $$ |
(5.16) |
N1 bezeichnet die Anzahl der auf dem ersten Niveau schwingenden Moleküle und N0 entsprechend die der nicht schwingenden Moleküle. Die Energiedifferenz zwischen erstem angeregtem Zustand E1 und Grundzustand E0 beträgt nach (5.15) h·f0. Wenn analog (4.12) der Entartungsgrad gV eingeführt wird, so wird aus (5.16):
| $$\frac{{N_1 }}{{N_0 }} = g_V \cdot e^{ - \frac{{h \cdot f_0 }}{{k_B \cdot T}}} $$ |
(5.17) |
Alle zweiatomigen Molekülschwingungen sind nicht entartet, das gleiche gilt für die Streckschwingungen des linearen CO2-Moleküls. Für diese Schwingungsarten ist gV = 1. Im Gegensatz dazu ist die Deformationsschwingung des CO2 zweifach entartet, weswegen in diesem Fall gV = 2 gesetzt werden muss. Tabelle 5-2 zeigt das Verhältnis N0:N1 für die Atmosphärenbestandteile bei verschiedenen Temperaturen.
| - |
O2: f0 = 46,63THz |
N2: f0 = 70,19THz |
CO2: f0(v1) = 38,55THz |
CO2: f0(v2) = 20,01THz |
CO2: f0(v3) = 70,47THz |
| N0:N1(+15°C) |
2370 |
120146 |
616 |
14 |
125885 |
| N0:N1(0°C) |
3631 |
228463 |
877 |
17 |
239990 |
| N0:N1(-20°C) |
6942 |
605950 |
1499 |
22 |
639005 |
| N0:N1(-44°C) |
17543 |
2446000 |
3226 |
33 |
2593828 |
Tab. 5-2: Verhältnis zwischen Grundzustand und erstem angeregten Zustand bei O2, N2 und CO2
Aus Tabelle 5-2 ist ersichtlich, dass auch bei der angenommenen Erdmitteltemperatur von +15°C Molekülschwingungen fast nicht vorkommen. Das erklärt die flache Kurve der Wärmekapazität cp bis etwa +100°C. Ab da werden dann Molekülschwingungen in der Luft in nennenswertem Umfang angeregt. Die Werte N0 und N1 beziehen sich jeweils auf Moleküle der gleichen Art. Wenn man wissen möchte, wie viele Moleküle bezogen auf die gesamte Luftmenge schwingen, muss die Konzentration c mit betrachtet werden. Für die Gesamtkonzentration cs der schwingenden Moleküle kann man schreiben:
| $$c_s = \sum\limits_i {\left( {c_i \cdot \frac{{N_{i1} }}{{N_{i0} }}} \right)}$$ |
(5.18) |
Mit den Zahlen aus Tabelle 5-2 und den Konzentrationen der einzelnen Gase in der Erdatmosphäre (siehe Kapitel 2) ergibt sich bei +15°C:
| $$c_s = \frac{{0,21}}{{2370}} + \frac{{0,78}}{{120146}} + \frac{{0,00038}}{{616}} + \frac{{0,00038}}{{14}} + \frac{{0,00038}}{{125885}} = 122,86ppm$$ |
|
Damit ein Molekül mittels elektromagnetischer Strahlung zum Schwingen angeregt werden kann, muss es entweder ein permanentes, oder zumindest ein veränderliches Dipolmoment besitzen. Das bedeutet, es müssen entweder verteilte Ladungsschwerpunkte von vorn herein vorhanden sein, oder aber sie müssen sich durch die Schwingung herausbilden. Alle homonuklearen zweiatomigen Moleküle, wie die hauptsächlichen Atmosphärenbestandteile N2 und O2, besitzen kein Dipolmoment und können somit auch nicht mit elektromagnetischer Strahlung in Wechselwirkung treten. Wie man in Abbildung 5-6 leicht sehen kann, besitzt CO2 wegen seines symmetrischen Aufbaus ebenfalls kein permanentes Dipolmoment. Führt das CO2-Molekül symmetrische Streckschwingungen v1 aus, so ändert sich nichts an der Verteilung der Ladungsschwerpunkte. Daher ist diese Schwingungsform genau wie bei den zweiatomigen homonuklearen Molekülen nicht infrarotaktiv.
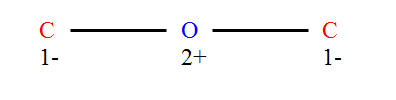
Abb. 5-6: Ladungsverteilung von CO2
Die Situation ändert sich bei der antisymmetrischen Streckschwingung und bei der Deformationsschwingung. Beide haben eine Änderung des Dipolmoments zur Folge, weshalb sie infrarotaktiv sind. Abbildung 5-7 zeigt die Deformationsschwingung v2, bei der die Ladungsverteilung zustande kommt, indem alle drei Atomkerne nicht mehr auf einer Linie liegen.
Diese CO2-Schwingung ist nach Tabelle 5-2 am höchsten thermisch angeregt, da ihre Eigenfrequenz mit f0(v2) = 20,01THz am niedrigsten liegt. Die durch die innermolekularen Bindungskräfte gebildete Federkonstante wird hier offenbar am schwächsten belastet. Die zugehörige Wellenlänge liegt bei:
| $$\lambda _0 (v2) = \frac{c}{{f_0 (v2)}} = \frac{{300000000\frac{m}{s}}}{{20,01 \cdot 10^{12} Hz}} = 15\mu m$$ |
(5.19) |
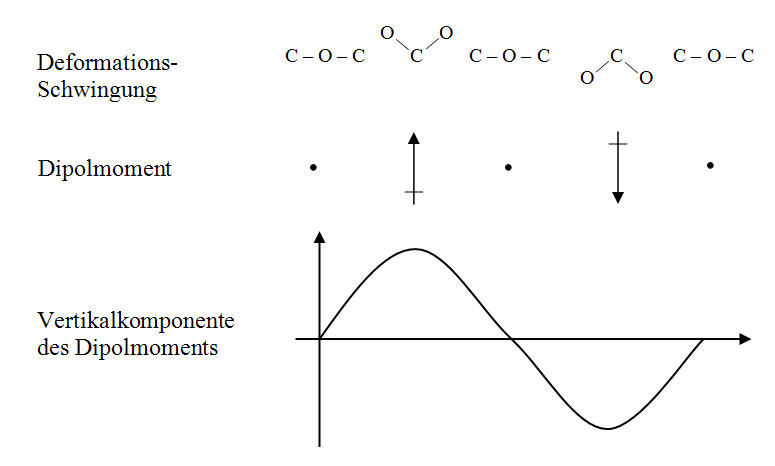
Abb. 5-7: Dipolwirkung der Deformationsschwingung von CO2
In Abbildung 5-1 erkennt man bei der roten 300K-Kurve der Erde bei 5…20μm die höchste Strahlungsintensität. Daraus lässt sich schlussfolgern, dass diese Schwingungsart wesentlich zum Treibhauseffekt beiträgt.
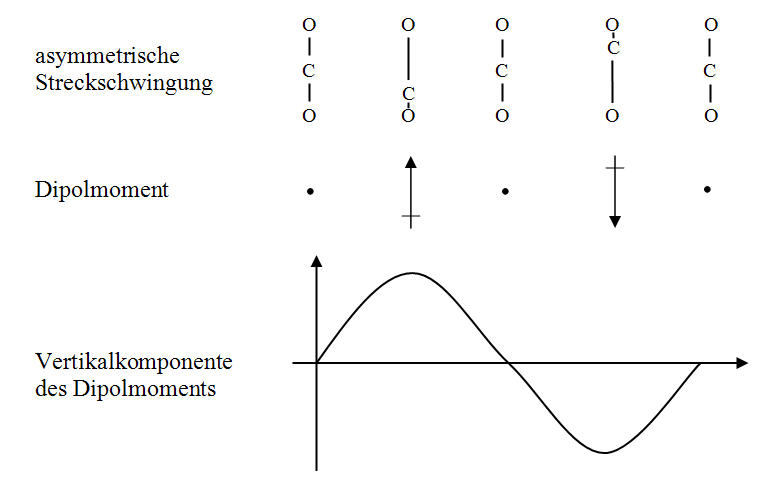
Abb. 5-8: Dipolwirkung der asymmetrischen Streckschwingung von CO2
In Abbildung 5-8 ist die asymmetrische Streckschwingung v3 des CO2-Moleküls dargestellt. Hier entsteht das Dipolmoment durch die lineare Verschiebung des Kohlenstoffatomkerns. Die thermische Anregung nach Tabelle 5-2 ist sehr gering, da die Eigenfrequenz mit f0(v3) = 70,47THz sehr hoch liegt. Die durch die innermolekularen Bindungskräfte gebildete Federkonstante wird hier offenbar am stärksten belastet. Die zugehörige Wellenlänge liegt bei:
| $$\lambda _0 (v3) = \frac{c}{{f_0 (v3)}} = \frac{{300000000\frac{m}{s}}}{{70,47 \cdot 10^{12} Hz}} = 4,2\mu m$$ |
(5.20) |
In Abbildung 5-9 ist die spektrale Ein- und Ausstrahlung der Erde dargestellt. Die Wellenlänge der Strahlung ist linear aufgetragen und die Strahlungsintensität logarithmisch. Die blaue Kurve zeigt die spektrale Verteilung des von der Erde empfangenen Sonnenlichts. Sie wurde mit (5.3) mit der Oberflächentemperatur der Sonne von 5770K berechnet. Nach (2.1) strahlt die Sonne an ihrer Oberfläche mit 62,85MW/m2. Nach (2.4) kommen davon noch 1368W/m2 als Solarkonstante auf der Erde an. Durch Division erhält man als Korrekturfaktor für (5.3) den Wert 0,0000218.
Die weinrote Kurve zeigt die spektrale Verteilung der von der Erdoberfläche bei 288K (+15°C) abgestrahlten Infrarotstrahlung.
Wie man sieht, beginnt die Ausstrahlung der Erde gerade bei 4μm. Die asymmetrische v3-Streckschwingung hat daher nur einen vernachlässigbar geringen Einfluss für den Treibhauseffekt. Die Erde ist sozusagen zu kalt für diese Schwingung. Sie hat wohl eher eine Filterwirkung für den langwelligen Anteil der Sonnenstrahlung und wird daher ähnlich dem Ozon zu einer Erwärmung der oberen Atmosphärenschichten beitragen. Die v2-Deformationsschwingung bei 15μm liegt dagegen voll im Ausstrahlungsbereich der Erde. Daher kann sie einen wesentlichen Beitrag zum Treibhauseffekt liefern.
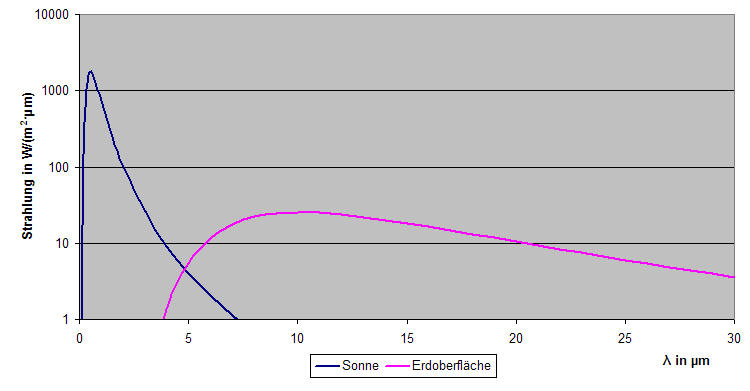
Abb. 5-9: spektrale Ein- und Ausstrahlung der Erde
|